Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo tính chất đường thẳng song song :
\(AK=KI=IH\)( gt )
=> AE = EM = MB
=> AF = FN = NC
Theo bài ra ta có : \(\frac{MN}{BC}=\frac{AM}{MB}=\frac{2MB}{MB}=2\)cm
\(\frac{EF}{BC}=\frac{AE}{EB}=\frac{AE}{2AE}=\frac{1}{2}\)cm
hay \(2EF=BC\)(*)
Ta có : \(S_{ABC}=\frac{1}{2}AH.BC=90\)( gt )
\(\Delta AMN\)có EF là đường trung bình ( AE = EM ; AF = FN )
Suy ra : EF // MN và EF = 1/2 MN
Ta có : \(S_{MNEF}=\frac{\left(EF+MN\right).IK}{2}\)mà \(IK=\frac{1}{3}AH\)
\(=\frac{\left(EF+MN\right).\frac{AH}{3}}{2}=\frac{\left(EF+2EF\right).\frac{AH}{3}}{2}\)
\(=\frac{EF.AH}{2}\)mà \(2EF=BC\)cmt (*)
\(=\frac{\frac{BC}{2}.AH}{2}=\frac{BC.AH}{4}\)
Vậy \(S_{MNEF}=\frac{180}{4}=45\)cm2

a) Áp dụng hệ quả định lý Ta-let ta có:
ΔABC có MN // BC (M ∈ AB, N ∈ AC) ⇒ 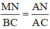
ΔAHC có KN // HC (K ∈ AH, N ∈ AC) ⇒ 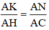
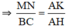
Chứng minh tương tự ta có:
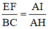
Mà ta có:
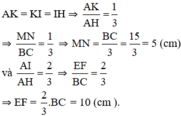
b) Ta có:


Sửa đề: Cho tam giác ABC có BC = 15 cm....a) tính MN và FE.
Giải:
a) Do \(\hept{\begin{cases}AK=KI=IH\\AK+KI+IH=AH\end{cases}}\Rightarrow AK=KI=IH=\frac{1}{3}AH\)
Có MK // BH; KN // HC. Theo hệ quả của định lí Thales:
\(\frac{MK}{BH}=\frac{AK}{AH}=\frac{KN}{HC}\). Hay: \(\frac{AK}{AH}=\frac{MK}{BH}=\frac{KN}{HC}=\frac{MK+KN}{BH+HC}=\frac{MN}{BC}\)
\(\Leftrightarrow\frac{MN}{BC}=\frac{1}{3}\Rightarrow MN=\frac{1}{3}BC=\frac{15}{3}=5\) cm.
*Tính FE:
Có: EI// BH; IF // HC. Theo hệ quả định lí Thales:
\(\frac{AI}{AH}=\frac{EI}{BH}=\frac{IF}{HC}=\frac{EI+IF}{BH+HC}=\frac{EF}{BC}\)
\(\Leftrightarrow\frac{EF}{BC}=\frac{2}{3}\Rightarrow EF=\frac{2}{3}BC=10cm\)
b) Ta có: \(S_{MNFE}=KI.\frac{MN+EF}{2}=\frac{1}{3}.AH.\frac{10+5}{2}=\frac{1}{3}.AH.\frac{BC}{2}\)
\(=\frac{1}{6}.AH.BC=\frac{1}{3}.\left(\frac{1}{2}.AH.BC\right)=\frac{1}{3}.S_{ABC}=\frac{1}{3}.270=90cm^2\)
Anh kiểm tra lại xem sao? Em mới học nên ko chắc.

$a)$ Vì $MN//EF//BC$ và \(AH\perp BC\)
Theo định lí Ta - lét, ta có: \(\dfrac{MN}{BC}=\dfrac{AK}{AH}=\dfrac{1}{3}\)
$\Rightarrow MN=\dfrac{BC}{3}=\dfrac{15}{3}=5(cm)$
Ta có: $\dfrac{EF}{BC}=\dfrac{2}{3} \Rightarrow EF =\dfrac{2}{3}.15=10(cm)$
$b)$ Ta có: $S_{ABC} = \dfrac{1}{2}AH.BC$
$\Rightarrow AH = \dfrac{2S_{ABC}}{BC}=\dfrac{2.270}{15}=36$
Mà $AI=IK=IH=\dfrac{1}{3}AH = \dfrac{36}{3}=12(cm)$
Vậy $S_{MNEF} = \dfrac{1}{2}(MN+EF).IK = \dfrac{1}{2}(5+10).12=90 (cm^2)$

a)
∆ABC có MN // BC.
=> = (kết quả bài tập 10)
Mà AK = KI = IH
Nên = => = => MN = BC = .15 = 5 cm.
∆ABC có EF // BC => = =
=> EF = .15 =10 cm.
b) Áp dụng kết quả ở câu b của bài 10 ta có:
SAMN= .SABC= 30 cm2
SAEF= .SABC= 120 cm2
Do đó SMNEF = SAEF - SAMN = 90 cm2
bt 10 là bt nào?
vs lại toàn Áp Dụng bài người khác, ko cm?!

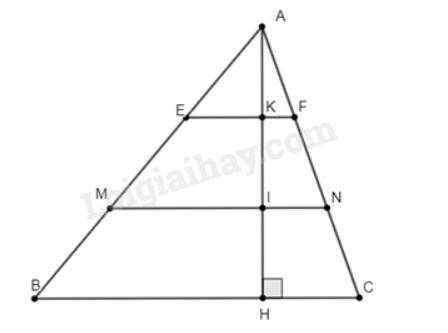
a) Vì \(AK = KI = IH \Rightarrow AK = \frac{1}{3}AH;AI = \frac{2}{3}AH\).
Vì \(EF//BC \Rightarrow EK//BH;MN//BC \Rightarrow MI//BH\)
Xét tam giác \(ABH\) ta có \(EK//BH\), theo định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{AK}}{{AH}} = \frac{1}{3}\)
Xét tam giác \(ABH\) ta có \(MI//BH\), theo định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}\)
Xét tam giác \(ABC\) ta có \(EF//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AE}}{{AB}} = \frac{{EF}}{{BC}} = \frac{1}{3} \Rightarrow \frac{{EF}}{{30}} = \frac{1}{3} \Rightarrow EF = \frac{{30.1}}{3} = 10\)
Xét tam giác \(ABC\) ta có \(MN//BC\), theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{30}} = \frac{2}{3} \Rightarrow EF = \frac{{30.2}}{3} = 20\)
Vậy \(EF = 10cm;MN = 20cm\).
b) Đổi \(10,8d{m^2} = 1080c{m^2}\)
Diện tích tam giác \(ABC\) là:
\({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}AH.30 = 1080\left( {c{m^2}} \right)\)
\( \Rightarrow AH = 1080.2:30 = 72cm\)
Ta có: \(AH \bot BC \Rightarrow AH \bot MN\) (quan hệ từ vuông góc đến song song)
Do đó, \(KI \bot MN\)
Mà \(KI = \frac{1}{3}AH \Rightarrow KI = \frac{1}{3}.72 = 24cm\)
Tứ giác \(MNFE\) có \(MN//EF\) (cùng song song với \(BC\)) nên tứ giác \(MNFE\) là hình thang.
Lại có: \(KI \bot MN \Rightarrow KI\)là đường cao của hình thang.
Diện tích hình thang \(MNFE\) là:
\({S_{MNFE}} = \frac{1}{2}\left( {EF + MN} \right).KI = \frac{1}{2}.\left( {10 + 20} \right).24 = 360\left( {c{m^2}} \right)\)
Vậy diện tích tứ giác \(MNFE\) là \(360c{m^2}\).
a:
Xét ΔABH có EK//BH
nên EK/BH=AK/AH=1/3
Xét ΔAHB có MI//BH
nên MI/BH=2/3
Xét ΔABC có MN//BC
nên AM/AB=MN/BC
=>MN/30=2/3
=>MN=20(cm)
Xét ΔABC có EF//BC
nên EF/BC=AE/AB=1/3
=>EF=10(cm)
b: S ABC=1/2*AH*BC
=>1/2*AH*30=1080
=>AH=1080/15=72(cm)
KI=1/3*AH=24(cm)
S MNFE=1/2*(EF+MN)*KI=360cm2

b) SABCD = \(\dfrac{1}{2}\) AH . BC
\(\Rightarrow\) 270 = \(\dfrac{1}{2}\) . AH . 15
\(\Rightarrow\) AH = \(\dfrac{270.2}{15}\) = 36 cm
Ta có AH = 3AK (câu a) và AK = KI (gt)
Do đó AH = 3KI
\(\Rightarrow\) KI = \(\dfrac{AH}{3}\) = \(\dfrac{36}{3}\) = 12 cm
SMNFE = \(\dfrac{1}{2}\) KI (MN + EF) = \(\dfrac{1}{2}\) . 12 (5 + 10) = 90 cm2
a) Ta có AH=AK+KI+IH và AK = KI = IH (gt)
\(\Rightarrow\) AH = 3AK\(\Rightarrow\) \(\dfrac{AK}{AH}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MK // BH (gt) \(\Rightarrow\) \(\dfrac{AM}{AB}\)= \(\dfrac{AK}{AH}\) \(\Rightarrow\) \(\dfrac{AM}{AB}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MN // BC (gt) \(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{AM}{BC}\)
\(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{1}{3}\)
\(\Rightarrow\) \(\dfrac{MN}{15}\)= \(\dfrac{1}{3}\)
\(\Rightarrow\) MN = \(\dfrac{15}{3}\) = 5 cm
...
∆AEI có MK // EI (gt) và K là trung điểm của AI (AK = KI)
\(\Rightarrow\) M là trung điểm của AE
Xét ∆AEF có MN // EF (gt)
\(\Rightarrow\) \(\dfrac{MN}{EF}\) = \(\dfrac{AM}{AE}\)
Mà \(\dfrac{AM}{AE}\) = \(\dfrac{1}{2}\) (M là trung điểm của AE)
Nên \(\dfrac{MN}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) \(\dfrac{5}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) EF = 10 cm
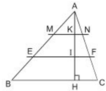

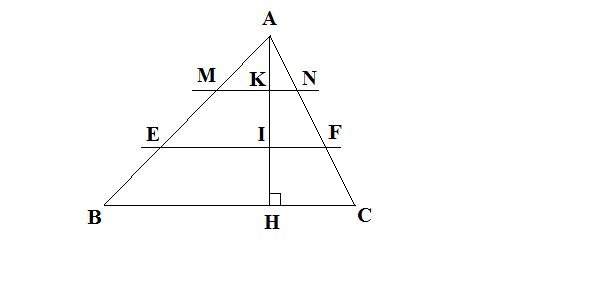 Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC
Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC