Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\left(c.cosC-b.cosB\right)=a.\left(c.\dfrac{a^2+b^2-c^2}{2ab}-b.\dfrac{a^2+c^2-b^2}{3ac}\right)\)
\(=\dfrac{\left(a^2+b^2-c^2\right)c^2}{2bc}-\dfrac{\left(a^2+c^2-b^2\right)b^2}{2bc}\)
\(=\dfrac{\left(b^2-c^2\right)\left(b^2+c^2-a^2\right)}{2bc}=\left(b^2-c^2\right)cosA\)

\(b.cosB+c.cosC=2R.sinB.cosB+2R.sinC.cosC\)
\(=R\left(sin2B+sin2C\right)=2R.sin\left(B+C\right)cos\left(B-C\right)\)
\(=2R.sinA.cos\left(B-C\right)=\frac{a}{sinA}.sinA.cos\left(B-C\right)=a.cos\left(B-C\right)\)

a.
Theo BĐT tam giác: \(c< a+b\Rightarrow c^2< ac+bc\)
\(b< a+c\Rightarrow b^2< ab+bc\) ; \(a< b+c\Rightarrow a^2< ab+ac\)
Cộng vế với vế: \(a^2+b^2+c^2< 2\left(ab+bc+ca\right)\)
b.
Do a;b;c là 3 cạnh của tam giác nên: \(\left\{{}\begin{matrix}a+b-c>0\\b+c-a>0\\c+a-b>0\end{matrix}\right.\)
\(\left(a+b-c\right)\left(b+c-a\right)\le\dfrac{1}{4}\left(a+b-c+b+c-a\right)^2=b^2\)
Tương tự: \(\left(b+c-a\right)\left(a+c-b\right)\le c^2\) ; \(\left(a+b-c\right)\left(a+c-b\right)\le a^2\)
Nhân vế với vế:
\(\left(abc\right)^2\ge\left[\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\right]^2\)
\(\Leftrightarrow abc\ge\left(a+b-c\right)\left(c+a-b\right)\left(b+c-a\right)\)

a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).

a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
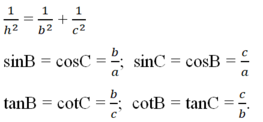

Chọn A.
Hệ thức trung tuyến xuất phát từ đỉnh A của tam giác:
![]()
Mà b2 + c2 = 2a2 nên ![]() nên
nên ![]() .
.

Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ a = 2 R . sin A
Tương tự, b = 2 R . sin B ; c = 2 R . sin C
Ta có: a b = c 2 n ê n 2 R . sin A . 2 R . sin B = ( 2 R sin C ) 2
Hay sin A . sin B = ( sin C ) 2
ĐÁP ÁN A

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
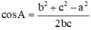
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
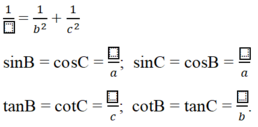
\(a\left(c.cosC-b.cosB\right)=a\left(c.\dfrac{a^2+b^2-c^2}{2ab}-b.\dfrac{a^2+c^2-b^2}{2ac}\right)\)
\(=\dfrac{\left(a^2+b^2-c^2\right).c^2}{2bc}-\dfrac{\left(a^2+c^2-b^2\right).b^2}{2bc}\)
\(=\dfrac{b^4-c^4+a^2c^2-a^2b^2}{2bc}\)
\(=\dfrac{\left(b^2-c^2\right)\left(b^2+c^2-a^2\right)}{2bc}=\left(b^2-c^2\right).cosA\)