Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là trung điểm BC, J là trung điểm DE. Do tam giác BEC vuông tại E mà EO là trung tuyến ứng với cạnh huyền nên OE = OB = OC. Tương tự OD = OB = OC. Từ đó ta có OE = OD hay tam tam giác OED cân tại O.
Lại có J là trung điểm DE nên \(OJ\perp DE\). Vậy thì OJ // BI // CK. Mà O là trung điểm BC nên OJ là đường trung bình hình thang CBKI. Vậy thì JI = JK.
Ta có \(JI=JK\Rightarrow JI-JE=JK-JD\Rightarrow EI=DK\left(đpcm\right)\)

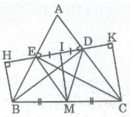
* Ta có: BH ⊥ DE (gt)
CK ⊥ DE (gt)
⇒ BH // CK hay tứ giác BHKC là hình thang
Gọi M là trung điểm của BC, I là trung điểm của DE
* Trong tam giác BDC vuông tại D có DM là trung tuyến ứng với cạnh huyền BC.
⇒ DM = 1/2 BC (tính chất tam giác vuông)
* Trong tam giác BEC vuông tại E có EM là đường trung tuyến ứng với cạnh huyền BC.
⇒ EM = 1/2 BC (tính chất tam giác vuông)
Suy ra: DM = EM nên ΔMDE cân tại M
MI là đường trung tuyến nên MI là đường cao ⇒ MI ⊥ DE
Suy ra: MI // BH // CK
BM = MC
Suy ra: HI = IK (tính chất đường trung bình hình thang)
⇒ HE + EI = ID + DK
Mà EI = ID nên EH = DK

Mình làm câu a thôi nha
a) Gọi M là trung điểm của BC , dễ dàng chứng minh được t/g MDE cân ở đỉnh M
Gọi I là trung điểm của DE thì MI vuông góc DE suy ra MI // BH // CE . MI là đường trung bình của hình thang BHKC có :
IH = IK
Từ đó suy ra IH - IE = IK - ID
nên HE = KD hay EH = DK ( đpcm )