Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
góc HBM=góc KCM
=>ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MB*MK

mik ko bt lm bài này bn à . mik thông minh lắm mấy bn mới ngu ấy

góc MKC=góc MIC=90 độ
=>MCKI nội tiếp
=>góc MIK+góc MCK=180 độ
góc MIB+góc MHB=180 độ
=>MIBH nội tiếp
=>góc MIH=góc MBH
góc MIH+góc MIK
=180 độ-góc MCK+góc MBH
=180 độ
=>H,I,K thẳng hàng

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

cho tam giác ABC vuông cân tại B.Trên cạnh BA và BC lấy hai điểm E và F sao cho BE = BF.Qua B và E kẻ đường vuông góc với AF,chúng cắt AC lần lượt ở I và K. EK cắt BC tại H
a)Chứng minh tam giác AHC cân
b)chứng minh I là trung điểm KC
c)Gọi M,N,P lần lượt là trung điểm EC,AF,EF

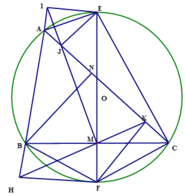
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )