Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE

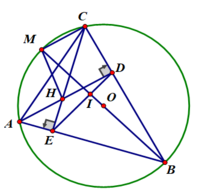
a) Xét tứ giác AEDC có:
∠(AEC) = ∠(ADC) = 90 0
Mà 2 góc này cùng nhìn cạnh AC
⇒ Tứ giác AEDC là tứ giác nội tiếp

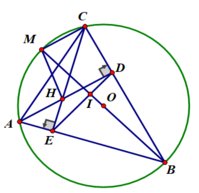
c) Do tứ giác AEDC là tứ giác nội tiếp nên ∠(CAB) = ∠(IDB) (cùng bù ∠(CDE) )
Mặt khác ∠(CAB) = ∠(CMB) (2 góc nội tiếp cùng chắn cung BC)
⇒ ∠(CMB) = ∠(IDB)
⇒ Tứ giác CMID là tứ giác nội tiếp ( Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)

Do BM là tiếp tuyến của đường tròn nên
Xét đường tròn (O) có AD là một dây cung. Lại có E là trung điểm AD nên theo tính chất của đường kính và dây cung, ta có hay .
Xét tứ giác OEBM có , chúng lại là hai góc kề nhau nên OEBM là tứ giác nội tiếp.
Cho tam giác có ba góc nhọn nội tiếp đường tròn tâm . Hai tiếp tuyến tại và cắt nhau tại . cắt đường tròn tại điểm thứ hai . Gọi là trung điểm đoạn . Chứng minh là tứ giác nội tiếp.

theo bai ta co là trung điểm đoạn

a) Ta có: \(\angle AEB=\angle ADB=90\Rightarrow ABDE\) nội tiếp
b) Vì AK là đường kính \(\Rightarrow\angle ACK=\angle ABK=90\)
\(\Rightarrow\left\{{}\begin{matrix}CK\bot AC\\BK\bot AB\end{matrix}\right.\) mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AC\end{matrix}\right.\Rightarrow\) \(BH\parallel CK,CH\parallel BK\)
\(\Rightarrow BHCK\) là hình bình hành
c) Vì F là giao điểm của CH và AB \(\Rightarrow CF\bot AB\)
Ta có: \(\dfrac{AD}{HD}+\dfrac{BE}{HE}+\dfrac{CF}{HF}=\dfrac{AD.BC}{HD.BC}+\dfrac{BE.AC}{HE.AC}+\dfrac{CF.AB}{HF.AB}\)
\(=\dfrac{S_{ABC}}{S_{HBC}}+\dfrac{S_{ABC}}{S_{AHC}}+\dfrac{S_{ABC}}{S_{AHB}}=S_{ABC}\left(\dfrac{1}{S_{HBC}}+\dfrac{1}{S_{AHC}}+\dfrac{1}{S_{AHB}}\right)\)
\(\ge S_{ABC}.\dfrac{9}{S_{HBC}+S_{HAC}+S_{AHB}}\)(BĐT Schwarz) \(=S_{ABC}.\dfrac{9}{S_{ABC}}=9\)
\(\Rightarrow Q_{min}=9\)

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

a) Xét tứ giác BNHM có
\(\widehat{BNH}\) và \(\widehat{BMH}\) là hai góc đối
\(\widehat{BNH}+\widehat{BMH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BNHM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
cậu ơi b,c luôn được không cậu