Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có:
BE ⊥ AC
KA ⊥ AC
=> BE // KA hay BH //KA (1)
Ta lại có:
KB ⊥ BC
AF ⊥ BC
=> KB // AF hay KB // AH (2)
Từ (1) (2) suy ra: AHBK là hình bình hành
b.
Xét ▲HAE và ▲HBF có:
góc AHE = BHF ( đối đỉnh)
Góc: E = F = 90o
Do đó: ▲HAE ~ ▲ HBF (g.g)
c.
Xét ▲CEB và ▲CFA có:
Góc C chung
Góc E = F = 90o
Do đó: ▲CEB~▲CFA (g.g)
=> \(\dfrac{CE}{CF}=\dfrac{CB}{CA}\Rightarrow CE.CA=CF.CB\)

a) AH // BK (cùng vuông góc BC)
AK // BH (cùng vuông góc AC)
=> Tứ giác AKBH là hình bình hành
b) Xét \(\Delta HAE\text{ và }\Delta HBF\text{ có }:\left\{{}\begin{matrix}\widehat{HEA}=\widehat{HFB}=90^o\\\widehat{AHE}=\widehat{BHF}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta HAE\sim\Delta HBF\)
c ) Xét \(\Delta BEC\text{ và }\Delta AFC\text{ có }:\left\{{}\begin{matrix}\widehat{BEC}=\widehat{AFC}=90^o\\\widehat{C}\text{ }chung\end{matrix}\right.\)
\(\Rightarrow\Delta BEC\sim\Delta AFC\Rightarrow\frac{CE}{CF}=\frac{CB}{CA}\Rightarrow CE\cdot CA=CB\cdot CF\)
d) Để tứ giác AHBK là hình thoi
thì => HK \(\perp AB\)
Mà CH \(\perp AB\) => C;H;K thẳng hàng.
Mà HK đi qua trung điểm AB
=> CH đi qua trung điểm AB
CH là đường cao đồng thời là đường trung tuyến
=> Tam giác ABC cân tại C.

) HS tự chứng minh AMBQ là hình chữ nhật (ahi đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
b) Sử dụng tính chất trực tâm tam giác.
c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh
P I = P Q = 1 2 A B .
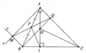
a) ta có: BK vuông góc với BC; AF vuông góc với BC
=> KB song song với AF hay KB song song với AH (1)
lại có: AK vuông góc với AC; BE vuông góc với AC
=> AK song song với BE hay AK song song với BH (2)
Từ (1)(2)=> tứ giác BKAH là hình bình hành (dấu hiệu 3)
b)Xét tam giác HAE và tam giác HBF có:
góc AHE = góc BHF (đối đỉnh);
góc AEH = góc BFH (= 900)
=> tam giác HAE đồng dạng với tam giác HBF (g-g)
c) Xét tam giác BEC và tam giác AFC có:
góc C chung; góc BEC = góc AFC (= 900)
=> tam giác BEC đồng dạng với tam giác AFC (g-g)
=> \(\dfrac{CE}{FC}=\dfrac{BC}{AC}\Rightarrow CE.AC=CF.CB\)