Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) cm : \(\Delta BHD\infty\Delta BCE\) \(\Rightarrow\frac{BH}{BC}=\frac{BD}{BE}\Rightarrow BH.BE=BC.BD\)
\(\Rightarrow BH.BE+BC.BD=BC.BD+BC.DC=BC^2\)
mà BC=2BM =>BC2=4BM2
=>\(\Rightarrow BH.BE+BC.DC=4BM^2\)
2) \(CM:\tan B=\frac{AD}{BD}\)
tan BHD =\(\frac{BD}{HD}\)
mà góc BHD= góc C
=>tan C=\(\frac{BD}{HD}\)
=> tanB.tanC=\(\frac{AD}{BD}.\frac{BD}{HD}=\frac{AD}{HD}\)

mk k bt đâu hưng vlog ạ ối dồi ôi
cái này giống toán 8 chứ k phải toán 9

a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông

∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2

a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
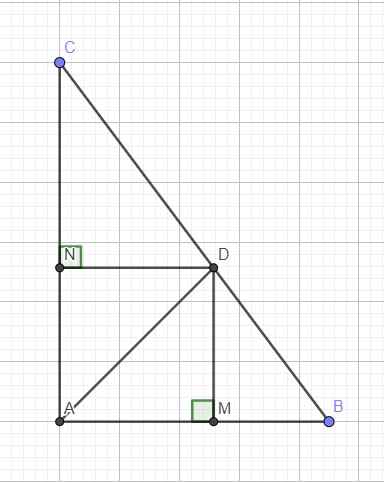
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)