Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. C/m: H,I,F thẳng hàng: Tứ giác HBMI nội tiếp ( vì I ,H cùng nhìn BM dưới 1 góc ngoài )
=>Góc HIB = góc HMB (1)
Tứ giác MICF nội tiếp ( góc I + góc F = 1800 )
=> Góc CIF = góc CMF (2)
Tứ giác ABMC nt ( O )
=> góc BAC + góc BMC = 1800
=> góc BAC + góc BMH + góc HMC = 1800 (3)
Tứ giác AHMF nội tiếp ( góc H + góc F = 1800 )
=> Góc HAC + góc HMF = 1800
=> Góc HAC + góc HMC + CMF = 1800 (4)
Từ (3), (4) => Góc BMH = Góc CMF (5)
Từ (1),(2),(5) => Góc HIB = góc FIC
Mà góc BIH + góc HIC = 1800 ( vì IB và IC là 2 tia đối )
=> Góc FIC + góc HIC = 1800nn=> IH và IF là 2 tia đối
=> H,I,F thẳng hàng
các bạn giải cho mình câu 3 thôi câu 1 , 2 mình biết làm rồi ạ

Hình bạn tự vẽ nha :v
a, áp dụng định lý pytago vào tam giác ABC có góc BAC =90 ta đc : BC2=AC2+AB2 thay vào là đc nha
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta dc :AH.BC=AB.AC thay vào là đc nha
Mà AM=1/2 BC thay vào nha :v
b, Xét tam giác ABE và tam giác ABF có : góc ABF - góc chung và góc AEB= góc BAF=90 => tam giác ABE đồng dạng tam giác FBA => BE/BA=AB/FB=> BE.FB=AB2(1)
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta đc : AB2 =BH.BC(2)
từ (1) và (2) => dpcm
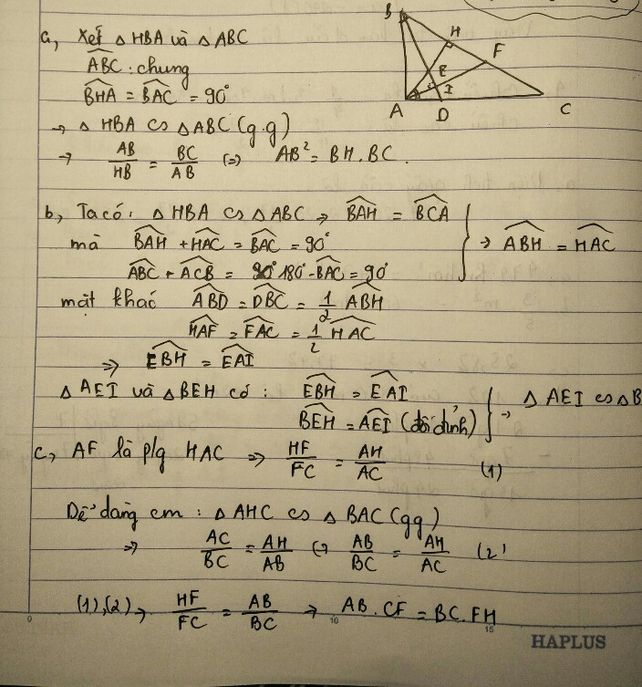
a,xét hai tam giác đòng dạng:ABH và ABC(g.g)
=>\(\dfrac{BH}{AB}\)=\(\dfrac{AB}{BC}\)=> đpcm
b,cm theo diện tích của tam giác vuông