Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

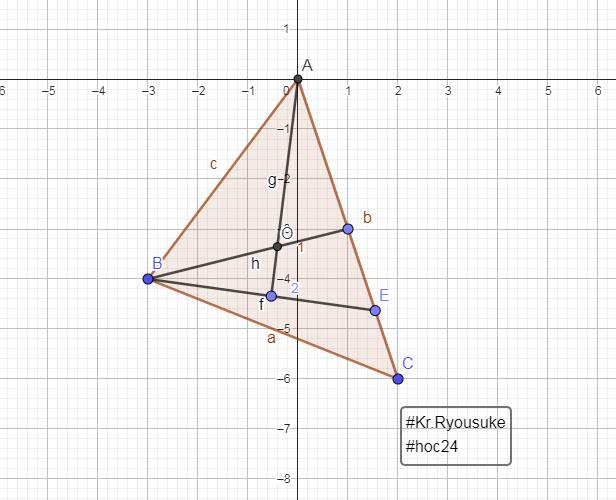
Vì các đường trung trực của `\Delta ABC` cắt nhau tại điểm O
`->` `\text {AO}` là đường trung trực thứ `3` của `\Delta`
Xét các đáp án trên `-> D.`

a: Xét ΔAOB và ΔCOE có
OB=OE
OA=OC
AB=CE
=>ΔAOB=ΔCOE
b: góc OAB=góc OCE
=>góc OAB=góc OAC
=>AO là phân giác của góc BAC

xét tg aob và coe
ab = ce
oa = oc ( thuộc đg trung trực ac )
ob = oe ( ............................. be )
suy ra hai tg =
b, vì hai tg trên =
-> góc oab = oce 1
tg aoc cân tại o
-.> góc oac = oce 2
từ 1,2 -> góc oab = oac
-> đpcm

Xét tam giác ABC, theo tính chất đường trung trực ta có:
OB = OE
OA = OC
Xét tam giác AOB và tam giác COE có:
AO = CO (cmt)
OB = OE (cmt)
AB = CE (gt)
=> tam giác AOB = Tam giác COA (c.c.c) (ĐPCM)
b)
Ta có: tam giác AOB = tam giác COE (ý a)
=> \(\widehat{ABO}=\widehat{CEO}\) (2 góc tương ứng)
Mà \(\widehat{CEO}=90^o\Rightarrow\widehat{ABO}=90^o\)
Lại có \(\widehat{AEO}=90^o\) (OC là đg trung trực)
Xét tam giác ABO và tam giác AEO có:
\(\widehat{ABO}=\widehat{AEO}=90^o\)
AO chung
BO = OE(cmt)
=> tam giác ABO = tam giác AEO (ch-cgv)
=> \(\widehat{BAO}=\widehat{EAO}\) (2 góc tương ứng)
hay \(\widehat{BAO}=\widehat{CAO}\)(do E \(\in\)AC)
Mà AO nằm giữa AB và AC
=> AO là tia phân giác của \(\widehat{BAC}\) (ĐPCM)
a. xét tgiac AOB và tgiac COE có:
AB=CE(gt)
OB=OE(tính chất đường trung trực)
OA=OC(tính chất đường trung trực)
vậy tgiac AOB=tgiac COE(c.c.c)
b. theo câu a ta có góc BAO= góc ECO(2 góc tương ứng) (1)
xét tgiac OHC và tgiac OHA có
OH chung
góc OHC= góc OHA=90
OC=OA(tính chất đuồng trung trực)
vậy Tgiac OHC=tgiac OHA(ch-cgv)
=> góc HCO= góc HAO(2 góc tương ứng )(2)
từ(1)và(2) ta có góc BAO= góc HAO
nên AO là tia phân giác của góc A