Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình tự vẽ nha bn! gọi K,I,P lần lượt là tđ của AB,AC,BC
ta có AG/AP=2/3=> S AMG/ABP=2/3=> AM/AB=2/3
ta có AM/AB=2/3,AG/AP=2/3=> MG//BP (định lý talet đảo)
khi MG//BP=> AB/AM=AP/AG (1)
khi GN//PC (MG//BP) => AP/AG=AC/AN (2)
từ (1),(2)=> AB/AM+AC/AN=2AP/AG=2.3/2=3

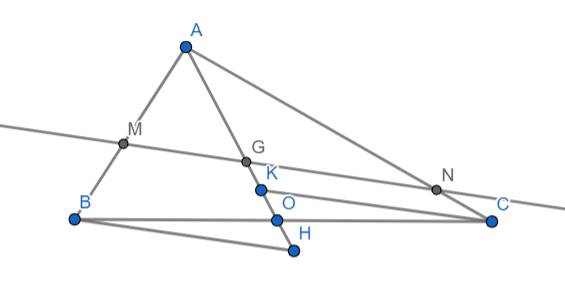
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)

a: XétΔABH và ΔACH có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
Do đó:ΔABH=ΔACH
b: Xét ΔABC có
AH là đường trung tuyến
BD là đường trung tuyến
AH cắt BD tại G
Do đó: G là trọng tâm của ΔABC
c: \(AH=\sqrt{15^2-9^2}=12\left(cm\right)\)
AG=2/3AH=8(cm)

a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)
Gọi J là trung điểm BC. Khi đó AJ là trung tuyến. Vậy thì AG = 2GJ. (1)
Xét tứ giác BIKC có BI cùng CK cùng song song với AG nên BI // CK hay BIKC là hình thang.
Xét hình thang BIKC có :
J là trung điểm BC
GJ // BI // KC
Suy ra GJ là đường trung bình hình thang BIKC.
Từ đó ta có: \(BI+CK=2GJ\) (2)
Từ (1) và (2) suy ra \(BI+KC=AG\)