Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
Do đó: ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
b: Kẻ HM//AB(M thuộc AC)
HN//AC(N thuộc AB)
Xét tứ giác AMHN có
AM//HN
AN//HM
Do đó: AMHN là hình bình hành
=>AM=HN; AN=HM
ΔAHM có AH<AM+MH
=>AH<AM+AN
HN//AC
mà BH vuông góc AC
nên HB vuông góc HN
ΔHBN vuông tại H
=>HB<BN
HM//AB
CH vuông góc AB
Do đó: HC vuông góc HM
=>ΔHCM vuông tại H
=>HC<MC
AH<AM+AN
HB<BN
HC<MC
=>HA+HB+HC<AM+AN+BN+MC=AC+AB
Chứng minh tương tự, ta được:
HA+HB+HC<AB+BC và HA+HB+HC<AC+BC
=>3*(HA+HB+HC)<2(BA+BC+AC)
=>HA+HB+HC<2/3*(BA+BC+AC)

Lời giải:
Xét tam giác $ABE$ và $ACF$ có:
$\widehat{A}$ chung
$AB=AC$ (gt)
$\widehat{AEB}=\widehat{AFC}=90^0$
$\Rightarrow \triangle ABE=\triangle ACF$ (ch-gn)
$\Rightarrow AE=AF$

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
FC=EB
Do đó: ΔFBC=ΔECB
Suy ra: \(\widehat{FCB}=\widehat{EBC}\)
=>ΔIBC cân tại I

a)vì ABC là tam giác vuông tại A
và AH vuông góc vs BC,dồng thời là đường cao,là đg trung tuyến trong tam giác
nên H=90độ
tam giác AHC vuông tại H

Do tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB}\)(tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
\(\widehat {ABC} = \widehat {ACB}\)
BC chung
=>\(\Delta BFC = \Delta CEB\)(cạnh huyền – góc nhọn)
=>\(CF=BE\) (2 cạnh tương ứng).

a) Tam giác ABE ( góc E=90 độ) và Tam giác ACF ( góc F=90 độ), có:
AB = AC ( gt )
Góc A chung
=> tam giác ... = tam giac ... ( cạnh huyền - góc nhọn)
=> BE = CF và góc ABE = góc ACF
b) Tam giác FCB ( góc F = 90 độ) và tam giác BEC ( góc E=90 độ), có:
BC chung
FC = EB ( c/m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> FB=EC
Tam giác ECI và tam giác FBI, có:
EC=FB (c/m trên)
góc E= góc F (=90 độ)
góc ACF = góc ABE (c/m trên)
=> tam giác ...= tam giác... (g-c-g)
c) Ta có: FA=AB - FB
EA=AC - EC
mà AB=AC; FB=EC
=> FA=EA
tam giác AIF(F=90 độ) tam giác AIE (E = 90 độ), có:
AI chung
FA=EA (c/ m trên)
=> tam giác... = tam giác... ( cạnh huyền-cạnh góc vuông)
=> góc BAI = góc CAI
hay AI là phân giác của góc A
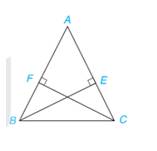
\(a,\)Xét \(\Delta ABE\)và \(\Delta ACF\)có :
\(\widehat{AEB}=\widehat{ACF}\left(gt\right)\)
\(AB=AC\left(gt\right)\)
\(\widehat{A}\)chung
\(\Rightarrow\Delta AEB=\Delta ACF\left(g.c.g\right)\)
\(\Rightarrow\widehat{ABE}=\widehat{ACF}\)( Hai góc tương ứng )
\(b,\)Ta có : \(\widehat{ABC}=\widehat{ABE}+\widehat{EBC}\)
\(\widehat{ACB}=\widehat{ACF}+\widehat{FCB}\)
Mà \(\widehat{ABC}=\widehat{ACB};\)\(\widehat{ABE}=\widehat{ACF}\left(cmt\right)\)
\(\Rightarrow\widehat{EBC}=\widehat{FCB}\)
\(\Rightarrow\Delta HBC\)cân tại H