K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 3 2020
https://h.vn/hoi-dap/question/168197.html
tham khảo nhé bạn

26 tháng 4 2022
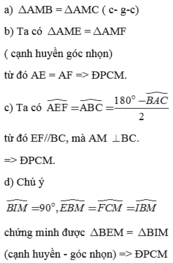
a) Xét △ABM và △ACM, có:
+ AB = AC
+ Góc BAM = góc CAM (AM là đường phân giác của △ABC)
+ AM cạnh chung
Vậy △ABM = △ACM (c-g-c)
b) Vì △ABM = △ACM
=> Góc AMB = góc AMC
Ta có: góc AMB + AMC = 1800
=> 1800 = 2AMB
AMB = \(\dfrac{180^0}{2}\) = 900
Vì AMB = AMC = 900
Suy ra: AM ⊥ BC
Vậy AM ⊥ BC
Câu c không biết làm nha bạn.

7 tháng 6 2022
a Xét ΔABM và ΔADM có
AB=AD
AM chung
BM=DM
Do đó: ΔABM=ΔADM
b: Ta có: ΔABD cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔABK và ΔADK có
AB=AD
\(\widehat{BAK}=\widehat{DAK}\)
AK chung
Do đó: ΔABK=ΔADK
Suy ra: KB=KD





Lời giải:
a. Tam giác ABM không cân bạn nhé. Tam giác ABD mới là tam giác cân.
Gọi $K$ là giao của $AM$ và $BD$
Xét tam giác $ABK$ và $ADK$ có:
$\widehat{BAK}=\widehat{DAK}$ (do $AK$ là phân giác $\widehat{BAC}$)
$\widehat{AKB}=\widehat{AKD}=90^0$
$AK$ chung
$\Rightarrow \triangle ABK=\triangle ADK$ (g.c.g)
$\Rightarrow AB=AD$
$\Rightarrow ABD$ là tam giác cân tại $A$
b. Xét tam giác $ABM$ và $ADM$ có:
$AM$ chung
$\widehat{BAM}=\widehat{DAM}$ (do $AM$ là phân giác $\widehat{BAC}$)
$AB=AD$ (cmt)
$\Rightarrow \triangle ABM=\triangle ADM$ (c.g.c)
c. Đề thiếu. Bạn xem lại.
Hình vẽ:
