Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Suy ra: \(\dfrac{AB}{HB}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)

a) áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(9^2+AC^2=15^2\)
\(81+AC^2=225\)
\(AC^2=144\)
\(AC=12\)
Ta có: \(AD+DC=AC\)( hình vẽ )
\(4,5+DC=12\)
\(DC=7,5\)
hình tự vẽ đi
d) Xét \(\Delta BAI\)và \(\Delta BDA\)có :
\(\widehat{ABD}\)( chung ) ; \(\widehat{AIB}=\widehat{BAD}=90^o\)
\(\Rightarrow\Delta ABI\approx\Delta DBA\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BI}=\frac{BD}{AB}\)\(\Rightarrow BI.BD=AB^2=81\)
Mà BH.BC = AB2 = 81 ( câu c )
\(\Rightarrow\)BI.BD = BH.BC
\(\Rightarrow\)\(\frac{BH}{BI}=\frac{BD}{BC}\)
Xét \(\Delta BHI\)và \(\Delta BDC\)có :
\(\frac{BH}{BI}=\frac{BD}{BC}\); \(\widehat{DBC}\)( chung )
\(\Rightarrow\Delta BHI\approx\Delta BDC\left(c.g.c\right)\)
\(\Rightarrow\widehat{BIH}=\widehat{BCD}\)hay \(\widehat{BIH}=\widehat{ACB}\)

a)
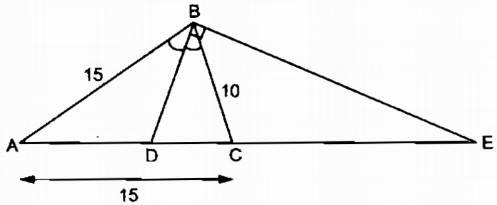
Vì BD là đường phân giác của \(\widehat{ABC}\) nên:
\(\frac{AD}{DC}=\frac{AB}{BC}\)(tính chất đường phân giác )
\(\Rightarrow\frac{AD}{AD+DC}=\frac{AB}{AB+BC}\)hay \(\frac{AD}{AC}=\frac{AB}{AB+BC}\)
Mà \(\Delta\)ABC cân tại A nên AC=AB=15cm
\(\Rightarrow\frac{AD}{15}=\frac{15}{15+10}\Rightarrow AD=\frac{15\cdot15}{25}=9\left(cm\right)\)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)

a) áp dụng định lí pitago vào tam giác abc được ab2 +ac2=bc2 suy ra bc2= 32+42=25 suy ra bc=5
có bd là phân giác góc abc nên ab/ad=bc/dc
dùng tính chất dãy tỉ số bằng nhau ta có ab/ad=bc/dc=(ab+bc)/(ad+dc)=(3+5)/4=2
nên ad=ab/2=3/2
dc=bc/2=5/2
b) dựa vào số đo độ đài cm được ec/ac=dc/bc
xét tam giác abc vuông và tam giác edc vuông có góc c chung và ea/ac=dc/bc nên suy ra 2 tam giác đó đồng dạng
c) tg abc và tg edc đồng dạng suy ra de vuông góc với bc
bd là phân giác abc có de vuông góc với bc, da vuông góc với ab nên suy ra de=da (tính châts này đã học ở lớp 7)
Tam giác ABC có AD là tia phân giác của BAC nên
\(\frac{DC}{DB}=\frac{AC}{AB}\)
=> \(\frac{DC}{DB+DC}=\frac{AC}{AB+AC}\)
=> \(\frac{35}{15+35}=\frac{DC}{BC}=\frac{DC}{40}\)
=> DC = 28 (cm)
Tam giác ABC có AE là tia phân giác của góc ngoài tại đỉnh A nên
\(\frac{AB}{AC}=\frac{EB}{EC}=\frac{EB}{EB+BC}=\frac{EB}{EB+40}\)
=> \(\frac{EB}{EB+40}=\frac{15}{35}\)
=> EB = 30 (cm)
Ta có:
ED = EB + BD = 30 + BC - CD = 30 + 40 - 28 = 42 (cm)