Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tg ABD và AED có: AE = AB (gt)
góc BAD = góc EAD
AD chung
DO đó tg ADB = tg AED (c.g.c)
=> BD = DE
=> tam giác BDE cân tại D (đcpm)

a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)
Xét ΔBED có BD=ED(cmt)
nên ΔBED cân tại D(Định nghĩa tam giác cân)
b) Ta có: AB=AE(gt)
nên A nằm trên đường trung trực của BE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DB=DE(cmt)
nên D nằm trên đường trung trực của BE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của BE
hay AD⊥BE tại trung điểm của BE
mà AD cắt BE tại I(gt)
nên AD⊥BE tại I
⇔\(\widehat{AIB}=90^0\)
Vậy: \(\widehat{AIB}=90^0\)
c) Ta có: ΔBDA=ΔEDA(cmt)
nên \(\widehat{BDA}=\widehat{EDA}\)(hai góc tương ứng)
mà tia DA nằm giữa hai tia DE,DB
nên DA là tia phân giác của \(\widehat{BDE}\)(đpcm)
a) Ta chứng minh được ΔABD = ΔAED (c-g-c)
=> BD = DE=> tam giác BDE cân tại D
b) Do ΔABD = ΔAED nên góc BDI = góc EDI
=> ΔBDI = ΔEDI (c-g-c)
=> góc BID = góc EID = 90 độ
=> góc AID = 90 độ
c) Ta có góc BDI = góc EDI
=> DA là phân giác của góc BDE

\(\text{#TNam}\)
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
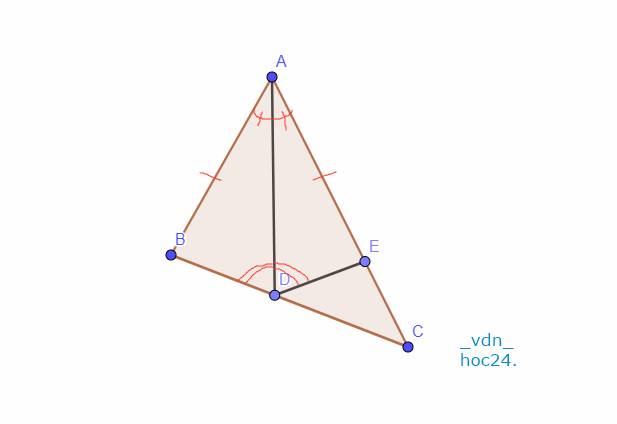

a:Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đo: ΔABD=ΔAED
=>DB=DE
b: ΔABD=ΔAED
nên góc BDA=góc EDA
=>DA là phân giác của góc BDE
c: Xét ΔDBI và ΔDEC có
BI=EC
góc DBI=góc DEC
DB=DE
Do đó: ΔDBI=DEC
=>góc BDI=góc EDC
=>góc BDI+góc BDE=180 độ
=>I,D,E thẳng hàng

Tự vẽ hình nha !
Xét tam giác ABD và tam giác AED có :
AB = AE ( giả thiết )
Góc BAD = góc EAD ( vì AD là tia phân giác góc BAC )
Cạnh AD chung
Suy ra tam giác ABD = tam giác AED ( c-g-c )
Do đó BD = DE ( 2 cạnh tương ứng ) hay tam giác BDE cân tại D
Vậy tam giác BDE cân tại D

a) Xét \(\Delta ABD\) và \(\Delta EBD:\)
BD chung.
\(\widehat{ABD}=\widehat{EBD}\) (BD là phân giác \(\widehat{B}).\)
\(\Rightarrow\Delta ABD=\Delta EBD\) (cạnh huyền - góc nhọn).
\(\Rightarrow\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^o\left(\widehat{BAC}=90^o\right).\)
\(\Rightarrow\widehat{BED}=90^o.\)
\(b)\Delta ABD=\Delta EBD\left(cmt\right).\\ \Rightarrow AB=EB.\)
Xét \(\Delta ABE:\)
\(AB=EB\left(cmt\right).\)
\(\Rightarrow\Delta ABE\) cân tại B (Tính chất tam giác cân).
Xét \(\Delta ABE\) cân tại B:
BD là phân giác \(\widehat{B}\left(gt\right).\)
\(\Rightarrow\) BD là trung trực của AE (Tính chất các đường trong tam giác cân).
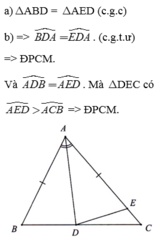
b, BAE cân tại A có AI là đường phân giác => AI là đường cao => AIB = 90 độ
c, phân giác