Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

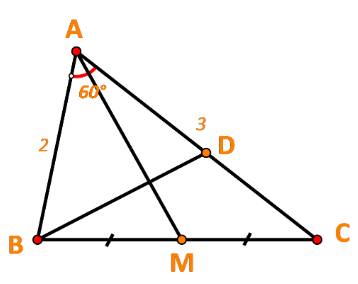
a) \(\overrightarrow {AB} .\overrightarrow {AC} = 2.3.\cos \widehat {BAC} = 6.\cos {60^o} = 3\)
b)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)(do M là trung điểm của BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
+) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} \)
c) Ta có:
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {BD} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right)\left( {\frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} } \right)\\ = \frac{7}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{7}{{24}}{\overrightarrow {AC} ^2} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \\ = - \frac{1}{2}A{B^2} + \frac{7}{{24}}A{C^2} - \frac{5}{{24}}\overrightarrow {AB} .\overrightarrow {AC} \\ = - \frac{1}{2}{.2^2} + \frac{7}{{24}}{.3^2} - \frac{5}{{24}}.3\\ = 0\end{array}\)
\( \Rightarrow AM \bot BD\)

\(BM=\dfrac{1}{2}BC=3\)
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cos60^0}=\sqrt{19}\)
\(BN=\dfrac{\sqrt{2\left(AB^2+BM^2\right)-AM^2}}{2}=\dfrac{7}{2}\)
A B → . A C → = A B . A C . cos A = 2.4. cos 60 ° = 2.4. 1 2 = 4 , A B → 2 = 4 , A C → 2 = 16
B N → . C M → = A N → − A B → . A M → − A C → = 1 2 A C → − A B → . 1 2 A B → − A C →
= 1 4 A C → . A B → − 1 2 A B → 2 − 1 2 A C → 2 + A C → . A B → = 5 4 A C → . A B → − 1 2 A B → 2 − 1 2 A C → 2
= 5 4 .4 − 1 2 .4 − 1 2 .16 = − 5
Chọn B