Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

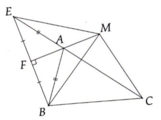
a: Xét tứ giác AEDB có
M là trung điểm chung của AD và EB
=>AEDB là hình bình hành
=>AE=DB và AE//DB
=>AE//BC
b: BD=AE
mà AE<AC
nên BD<AC
c: Xét tứ giác AFDC có
M là trung điểm chung của AD và FC
=>AFDC là hình bình hành
=>AF//DC
mà AE//DC
nên A,E,F thẳng hàng
Cho mik hỏi chút với ạ, làm sao bạn chứng minh được AE<AC ạ?

a: ΔACB cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{FCN}\)(hai góc đối đỉnh)
nên \(\widehat{ABC}=\widehat{FCN}\)
Xét ΔEBM vuông tại M và ΔFCN vuông tại N có
BM=CN
\(\widehat{EBM}=\widehat{FCN}\)
Do đó: ΔEBM=ΔFCN
=>EM=FN
b: ED//AC
=>\(\widehat{EDB}=\widehat{ACB}\)(hai góc đồng vị)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{EDB}=\widehat{ABC}\)
=>\(\widehat{EBD}=\widehat{EDB}\)
=>ΔEBD cân tại E
ΔEBD cân tại E
mà EM là đường cao
nên M là trung điểm của BD
=>MB=MD
c: EM\(\perp\)BC
FN\(\perp\)BC
Do đó: EM//FN
Xét ΔOME vuông tại M và ΔONF vuông tại N có
ME=NF
\(\widehat{MEO}=\widehat{NFO}\)(hai góc so le trong, EM//FN)
Do đó: ΔOME=ΔONF
=>OE=OF

b1 :
tự cm tam giác ABC vuông
=> góc ABC + góc ACB = 90 (đl)
BI là pg của góc ABC => góc IBC = góc ABC : 2
CI là pg của góc ACB => góc ICB = góc ACB : 2
=> góc IBC + góc ICB = (góc ABC + góc ACB) : 2
=> góc IBC + góc ICB = 45
xét tam giác IBC => góc IBC + góc ICB + góc BIC = 180
=> góc BIC = 135