Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{m}=2\left(1;2\right)+3\left(3;4\right)=\left(2;4\right)+\left(9;12\right)=\left(11;16\right)\)

a) Gọi \(M\left( {a;b} \right) \Rightarrow \overrightarrow {AM} = \left( {a - 2;b - 3} \right)\)
Tọa độ vecto \(\overrightarrow {BC} = \left( {4; - 2} \right)\)
Để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 4\\b - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 1\end{array} \right.\)
Vậy để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) thì tọa độ điểm M là:\(M\left( {6;1} \right)\)
b) Gọi \(N\left( {x,y} \right) \Rightarrow \overrightarrow {NC} = \left( {3 - x, - 1 - y} \right)\)và \(\overrightarrow {AN} = \left( {x - 2,y - 3} \right)\)
Do N là trung điểm AC nên \(\overrightarrow {AN} = \overrightarrow {NC} \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 3 - x\\y - 3 = - 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = 1\end{array} \right.\) . Vậy \(N\left( {\frac{5}{2},1} \right)\)
Ta có: \(\overrightarrow {BN} {\rm{ }} = \left( { \frac{7}{2};0} \right)\) và \(\overrightarrow {NM} = \left( {\frac{{ 7}}{2};0} \right)\). Vậy \(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \)

Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong

Chị ơi giúp e cái này tìm 3 giá trị của x sao cho 0,6<x<0,61
Gọi I là tâm đường tròn nội tiếp tam giác ABC
\(\Rightarrow a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\)
Ta có:
\(A=\left|a\overrightarrow{MA}+b\overrightarrow{MB}+c\overrightarrow{MC}\right|=\left|\left(a+b+c\right)\overrightarrow{MI}+a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right|\)
\(=\left|\left(a+b+c\right)\overrightarrow{MI}\right|=\left(a+b+c\right).MI\)
\(Amin\Leftrightarrow MImin\)
\(\Leftrightarrow\) M trùng I

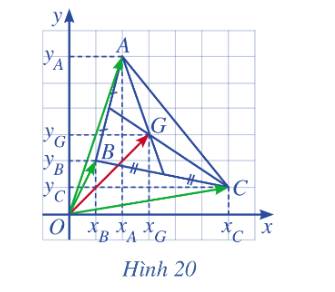
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

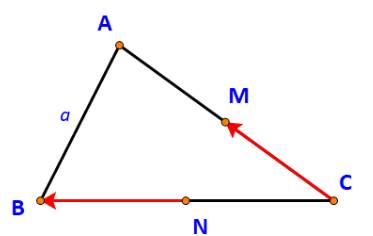
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)
\( \Rightarrow \overrightarrow {NC} = - \overrightarrow {NB} \)
Do đó: \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} = \overrightarrow {NC} + \overrightarrow {CM} \)(tính chất giáo hoán)
\( \Rightarrow \overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {NM} \Leftrightarrow \;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)
Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)
Vậy \(\;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \frac{a}{2}.\)

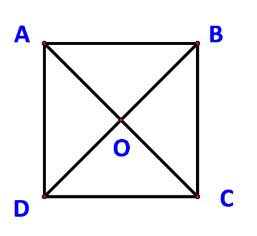
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \)
\( \Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)
b) Ta có: \(\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)
c) Ta có: \(\overrightarrow {DO} = \overrightarrow {OB} \)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA} \)
\( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)
a) \(\overrightarrow{AB}\)=(-1-2;2-1)
<=>\(\overrightarrow{AB}\)(-3;1)
b) ta có:
D(x;y)\(\left\{{}\begin{matrix}3\left(-3\right)-2\left(x-\left(-1\right)\right)+x-3=0\\3.1-2\left(y-2\right)+y-4=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}-9-2x-2+x-3=0\\3-2y+4+y-4=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}-x-14=0\\-y+3=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=-14\\y=3\end{matrix}\right.\)
vậy D(-14;3)