Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

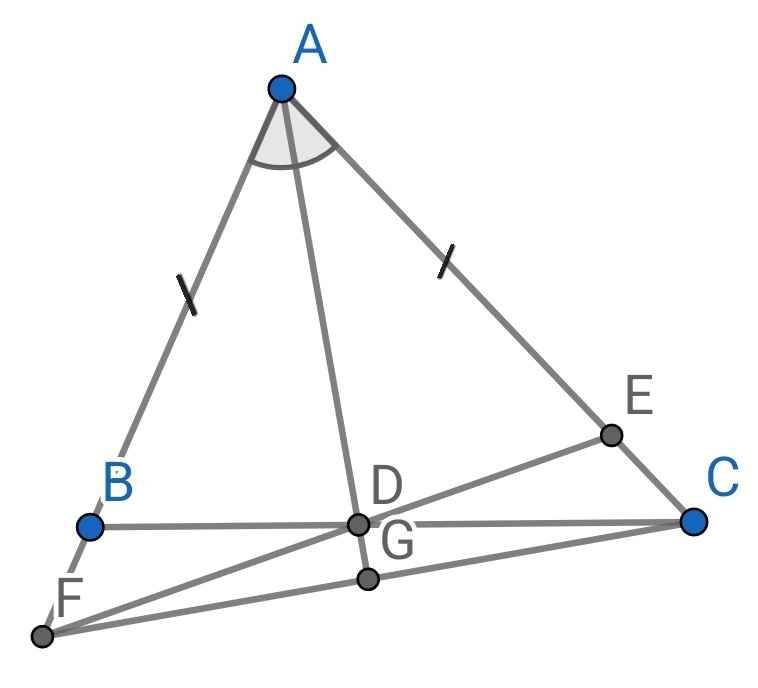 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ BD = ED (hai cạnh tương ứng)
Do ∆ABD = ∆AED (cmt)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
Ta có:
∠ABD + ∠FBD = 180⁰ (kề bù)
∠AED + ∠CED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Xét ∆BDF và ∆EDC có:
BD = ED (cmt)
∠FBD = ∠CED (cmt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (g-c-g)
b) Do ∆BDF = ∆EDC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
c) Gọi G là giao điểm của AD và CF
AG là tia phân giác của ∠FAC
⇒ ∠FAG = ∠CAG
Xét ∆AFG và ∆ACG có:
AF = AC (gt)
∠FAG = ∠CAG (cmt)
AG là cạnh chung
⇒ ∆AFG = ∆ACG (c-c-c)
⇒ ∠AGF = ∠AGC (hai góc tương ứng)
Mà ∠AGF + ∠AGC = 180⁰ (kề bù)
⇒ ∠AGF = ∠AGC = 180⁰ : 2 = 90⁰
⇒ AG FC
Hay AD ⊥ FC

bạn tham khảo bài này nhé : https://olm.vn/hoi-dap/detail/100443553347.html

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}\)
\(\Leftrightarrow\widehat{ACB}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(\widehat{ACB}=30^0\)
b) Xét ΔADB và ΔEDB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔADB=ΔEDB(c-g-c)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
c) Ta có: BE+EC=BC(E nằm giữa B và C)
BA+AM=BM(A nằm giữa B và M)
mà BE=BA(ΔBED=ΔBAD)
và BC=BM(gt)
nên EC=AM
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔDAB=ΔDEB)
AM=EC(cmt)
Do đó: ΔADM=ΔEDC(hai cạnh góc vuông)
nên \(\widehat{ADM}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADM}+\widehat{ADE}=180^0\)
\(\Leftrightarrow\widehat{EDM}=180^0\)
hay E,D,M thẳng hàng(đpcm)

Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC