Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



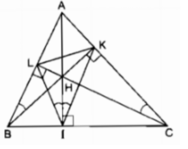
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác BIHL nội tiếp.

Tứ giác CIHK nội tiếp.

Từ (1), (2) suy ra:
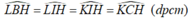

Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có ![]()
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có ![]()
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có ![]()
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có ![]()
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có ![]()
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có 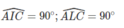
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.

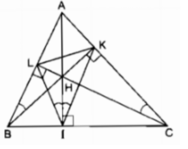
Vì ∆ ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.


a: Xét tứ giác BFEC có góc BFC=góc BEC=90 độ
nên BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>CK//AH
Xét (O) có
ΔBAK nội tiếp
BK là đường kính
Do đó: ΔBAK vuông tại A
=>AK//CH
Xét tứ giác CHAK có
CH//AK
CK//AH
DO đó: CHAK là hình bình hành

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

a) Có ^AOB = 1800 - ^OAB - ^OBA = 1800 - ^BAC/2 - ^ABC/2 = 900 + (1800 - ^BAC - ^ABC)/2 = 900 + ^ACB/2
b) Dễ thấy A,M,O,E cùng thuộc đường tròn đường kính OA (Vì ^AMO = ^AEO = 900) (1)
Ta có ^AOK = 1800 - ^AOB = 1800 - (900 + ^ABC/2) = 900 - ^ACB/2 = ^CEN (Do \(\Delta\)CEN cân tại C)
=> Tứ giác AOKE nội tiếp hay A,O,K,E cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra năm điểm A,M,K,O,E cùng thuộc một đường tròn (đpcm).
c) Ta thấy A,O,K,E cùng thuộc một đường tròn (cmt) và OK cắt AE tại T
Nên \(\frac{KT}{ET}=\frac{AT}{OT}\)(Hệ thức lượng đường tròn). Kết hợp \(\frac{AT}{OT}=\frac{AB}{OB}\)(AO là phân giác ^BAT)
Suy ra \(\frac{KT}{ET}=\frac{AB}{OB}\). Mặt khác: ^BKN = ^OAE = ^BAO và ^NBK = ^OBA => \(\Delta\)BKN ~ \(\Delta\)BAO (g.g)
=> \(\frac{AB}{OB}=\frac{KB}{NB}\). Từ đây \(\frac{KT}{ET}=\frac{KB}{BN}\)=> KT.BN = KB.ET (đpcm).

a) Ta có: \(\angle AKB=\angle AIB=90\Rightarrow AKIB\) nội tiếp
b) Trong (O) có DE là dây cung không đi qua O và M là trung điểm DE
\(\Rightarrow OM\bot DE\)
CEAD nội tiếp \(\Rightarrow\angle CED=\angle CAD\)
CEBD nội tiếp \(\Rightarrow\angle CDE=\angle CBE\)
mà \(\angle CAD=\angle CBE\) (AKIB nội tiếp)
\(\Rightarrow\angle CED=\angle CDE\Rightarrow\Delta CDE\) cân tại C mà M là trung điểm DE
\(\Rightarrow CM\bot DE\Rightarrow C,O,M\) thẳng hàng
c) AKIB nội tiếp \(\Rightarrow\angle IKB=\angle IAB=\angle DAB=\angle DEB\)
\(\Rightarrow\) \(IK\parallel DE\)