Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\Delta ABE,\Delta ACF\) có \(\widehat{A}\) chung và \(\widehat{AEB}=\widehat{AFC}\left(=90^o\right)\) nên suy ra \(\Delta ABE~\Delta ACF\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\Rightarrow AB.AF=AC.AE\).
b) Từ \(AB.AF=AC.AE\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\). Từ đó suy ra \(\Delta AEF~\Delta ABC\left(c.g.c\right)\) \(\Rightarrow\widehat{AFE}=\widehat{ACB}\)
c) Xét tam giác AEF có \(C\in AE,B\in AF,K\in EF\) và \(K,B,C\) thẳng hàng nên áp dụng định lý Menelaus, ta có \(\dfrac{KF}{KE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\) (1).
Mặt khác, cũng trong tam giác AEF, có \(C\in AE,B\in AF,I\in EF\) và AI, EB, FC đồng quy nên theo định lý Ceva, \(\dfrac{IF}{IE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\) (2).
Từ (1) và (2), suy ra \(\dfrac{KF}{KE}=\dfrac{IF}{IE}\Leftrightarrow KF.IE=KE.IF\)

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AB}{AE}=\dfrac{AC}{AF}\)
Xét ΔABC và ΔAEF có
\(\dfrac{AB}{AE}=\dfrac{AC}{AF}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔABC\(\sim\)ΔAEF(c-g-c)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F co
góc A chung
=>ΔAEB đồng dạng với ΔAFC
b: ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF

Bài 1:
a) Xét tam giác ABE và tam giác ACF có:
Góc AEB=góc AFC(=90 độ)
Góc A chung
=>Tam giác ABE đồng dạng vs tam giác ACF (g-g)
b)
Vì tam giác ABE đồng dạng vs tam giác ACF(cmt)
=>\(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác AFE và tam giác ACB có:
Góc A chung(gt)
\(\frac{AB}{AC}=\frac{AE}{AF}\)
=>Tam giác AFE và tam giác ACB đồng dạng (c-g-c)
c)
H ở đou ra vại? :))

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AE/AB=AF/AC và AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ACB
c; góc AFH=góc AEH=90 độ
=>AFHE nội tiếp (I)
=>IF=IE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp (M)
=>MF=ME
=>MI là trung trực của EF
=>MI vuông góc EF


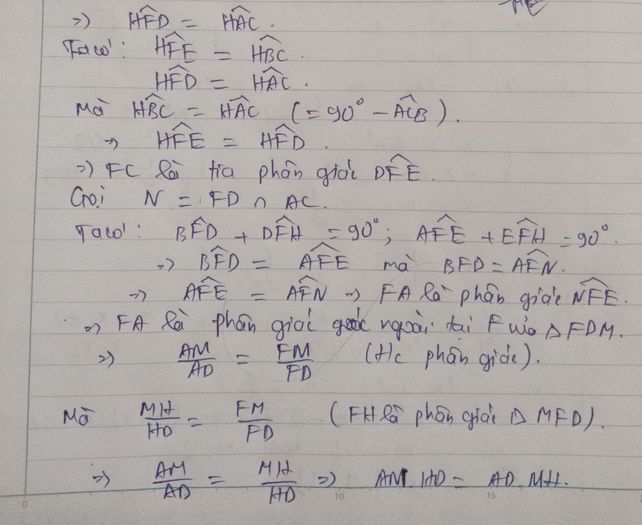 Bạn tham khảo cách làm nhé!
Bạn tham khảo cách làm nhé!