Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

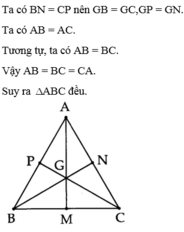
- Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.
Do đó, AM có là đường trung tuyến của tam giác ABC
- Ta có:
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)

Tự vẽ hình nha ;-;
a) Gọi AG cắt BC tại D
Tam giác ABC cân tại A, G là trọng tâm tam giác
=> AD vừa là đường trung tuyến, vừa là đường phân giác
=> AG là tia phân giác của góc BAC
b) Xét tam giác NBC và tam giác MCB có
BC chung
NBC=MCB ( do tam giác ABC cân tại A )
BN=CM ( tam giác ABC cân tại A => AB=AC => 1/2 AB= 1/2 AC)
=> Tam giác NBC= tam giác MCB ( c.g.c)
=> NC= MB
=> 1/3 NC =1/3 MB
( do G là trọng tâm tam giác ABC)
=> GN= GM