Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

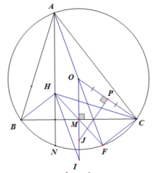
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)

Sửa đề: Đường cao BD
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}\left(=90^0\right)\)
Do đó: BEDC là tứ giác nội tiếp
hay B,E,D,C cùng thuộc 1 đường tròn
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AD\cdot AC=AE\cdot AB\)

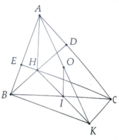
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM

a, Vì I đối xứng với H qua AC => \(\widehat{AIC}=\widehat{AHC}=90^o\)=>\(\widehat{AIC}+\widehat{AHC}=180^o\)=> AICH nội tiếp
b, Vì I đối xứng với H qua qua AC=> AI=AH
Vì I đối xứng với K qua qua AB=>AK=AH=> AI=AK
c,\(\widehat{KHB}=\widehat{ECB}\)vì cùng phụ với góc ABC (AB vuông góc với KH)
=> KH//CE. Mà CE vuông góc với AB=> CE vuông góc với AB => góc CEA =90 độ
=> Góc CEA= góc CHA =90 độ => AEHC nội tiếp. Mà AICH nội tiếp (theo a)
=> 5 điểm A,E,H,C,I cùng thuộc 1 đường tròn