Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

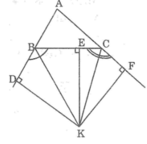
Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.
Kẻ KE ⊥ BC, KF ⊥ AC, KD ⊥ AB
Vì K nằm trên phân giác của ∠(CBD) nên:
KD = KE (tính chất tia phân giác) (1)
Vì K nằm trên tia phân giác của ∠(BCF) nên:
KE = KF (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: KD = KF
Điểm K nằm trong ∠(BAC) cách đều 2 cạnh AB và AC nên K nằm trên tia phân giác của ∠(BAC) .

Gọi K là giao điểm của hai đường phân giác góc ngoài tại B và C
Kẻ KE,KD,KF vuông góc lần lượt với BC,AB,AC
Xét ΔBDK vuông tại D và ΔBEK vuông tại E có
KB chung
\(\widehat{DBK}=\widehat{EBK}\)
Do đó: ΔBDK=ΔBEK
Suy ra: KD=KE(1)
Xét ΔCEK vuông tại E và ΔCFK vuông tại F có
CK chung
\(\widehat{ECK}=\widehat{FCK}\)
Do đó;ΔCEK=ΔCFK
Suy ra: KE=KF(2)
Từ (1) và (2) suy ra KD=KF
hay K nằm trên đường phân giác của góc A(Đpcm)

bạn tự kẻ hình nhé :))
gọi I là giao điểm của đường phân góc ngòai tại góc B và góc C
vẽ IH vuông với Bx
IK vuông với BC
IL vuông với Hy
I € đường phân giác góc ngoài góc B
=> IK = IH (1)
I € đường phân giác góc ngoài góc C
=> IH = IL (2)
Từ (1) và (2) => IK = IL
=> I € tia phân giác góc A
Vậy : tia phân giác góc ngoài tại góc B,C và tia phân giác góc A cùng đi qua một điểm
gọi giao của hai đường phân giác ngoài tại B và C là G
Kẻ GL vuông góc với AB,GK vuông góc với AC,GJ vuông góc với BC
Vì BG là tia phân giác của B=>GL=GJ (1)
Vì CG là phân giác của C=>GJ=GK (2)
Từ (1) và (2) =>GL=GK
=>AG là tia phân giác của A
=>CG,BG,AG đi qua cùng một điểm
Vậy 2 đường phân giác ngoài tại B và C và đường phân giác trong đi qua cùng một điểm