Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(B_1\equiv E;A_1\equiv F\)
Xét ΔEAB vuông tại E và ΔFBA vuông tại F có
AB chung
\(\widehat{EAB}=\widehat{FBA}\)
Do đo; ΔEAB=ΔFBA
Suy ra: \(\widehat{MBA}=\widehat{MAB}\)
=>ΔMAB cân tại M
=>MA=MB
mà CA=CB
nên CM là đường trung trực của AB

đề bài nhầm rồi từ A kéo đến b ko vuông góc với ab nha

a) Xét tam giác BEM và tam giácCFM
có:BM=MC(gt)
góc EBM=gócFCM(tam giác ABC can^)
->T/g BEM=t/g CFM(c.huyền g. nhon)
b)
Xét tam giác vg AEM va t/g vg AFM
có:EM=MF(t/g BEM=t/gAFM)
AM là cạnh chung
->t/g AEM =t/g AFM( c/ huyền -c.góc vg)
->AE=AF(2 cạnh tương ứng)
Xét tam giác AEI và t/g AFI
có:MF=EM(t/g BEM= t/g CFM)
AM là cạnh chung
AF=AE(C/ m trên)
->t/g AEI =t/g AFI(c-c-c)
->EI = IF(2 cạnh tương ứng)
->góc AIE= góc AIF(2 tương ứng)
=>AE là đường trung trực của EF
c(mik ko pt lm)
a và b bạn Hương Sơn
c) Ta có:
\(\Delta ABC\)cân
có AM là đường trung tuyến
=> AM cũng là đường trung trực
=> \(AM\perp BC\)
=> AM = 90 độ
Vì \(\Delta ABC\)cân
=> Góc ABM = góc ACM (1)
mà Góc ABD = góc ACD = 90 độ (2)
Từ (1) và (2) => Góc MBD = góc MCD
Xét \(\Delta DMB\)và \(\Delta DMC\)có :
DM : cạnh chung (1)
Góc MBD = góc MCD ( chứng minh trên ) (2)
BM = MC ( vì AM là đường trung tuyến của tam giác ABC ) (3)
Từ (1) ; (2) và (3) => \(\Delta DMB=\Delta DMC\)(cạnh - góc - cạnh)
=> Góc CMD = góc BMD ( cặp góc tương ứng)
Mà Góc CMD + góc BMD = 180 độ
=> Góc CMD = BMD = 180 : 2 = 90 độ
Vì Góc AMC = 90 độ ( vì AM là đường trung trực)
và góc CMD = 90 độ
=> AMC + CMD = AMD
=> 90 + 90 = AMD
=> AMD = 180 độ
=> Ba điểm A ; M ; D thẳng hàng. ( điều phải chứng minh)
Chúc bạn học tốt !

d) △ABC đều có: CD là đường cao \(\Rightarrow\)CD cũng là phân giác.
\(\Rightarrow\widehat{BCD}=\widehat{ACD}\).
Mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{IBC}\\\widehat{ACD}=\widehat{CIB}\end{matrix}\right.\) (DC//BI)
\(\Rightarrow\widehat{IBC}=\widehat{CIB}\)
\(\Rightarrow\)△BCI cân tại C.
mình mới nghĩ được đến đây, rất xin lỗi bạn, vẫn còn ý đầu của câu d, nếu mình nghĩ ra sẽ làm giúp bạn nha




a) Chứng minh:BEM=CFM
Xét tam giác BEM và tam giác CFM, có:
- góc BEM = góc CFM = 90 độ (do ME vuông góc AB; MF vuông góc AC)
- MB = MC (AM là trung tuyến, trung trực của tam giác ABC)
- góc B = góc C (do tam giác ABC cân tại A)
=> tam giác BEM và tam giác CFM (tam giác vuông có cạnh huyền, góc nhọn bằng nhau) (đpcm)
b)Chứng minh: AM là trung trực của EF
Gọi I là điểm giao nhau của AM và EF
Xét tam giác AEI và tam giác AFI, có
- AE = AF (do AE = AB - EB, AF = AC - FC; mà AB = AC co tam giác ABC cân, EB = FC do tam giác BEM = tam giác CFM)
- góc EAI = góc FAI (do AM là trung tuyến, trung trực, phân giác của tam giác cân ABC)
- cạnh AI chung
=> tam giác AEI = tam giác AFI
=> AR = AF =>tam giác AEF cân tại F (1)
Thêm nữa: IE = IF => I là trung điểm của EF (2)
Từ (1) và (2) => AI là trung tuyến của tam giác cân AEF, và cũng là là trung trực của tam giác AEF
=> AI vuông góc EF tại I
mà A,I,M thẳng hàng
=> AM là trung trực của EF
c) Từ B kẻ đường thẳng vuông góc với AB tại B,từ C kẻ đường thẳng vuông góc với AC tại C,hai đường thẳng này cắt nhau tại D.Chứng minh rằng ba điểm A,M,D thẳng hàng
Xét tam giác vuông ABD và tam giác vuông ACD, có
- AB = AC
- BAD = CAD
- AD chung
=> tam giác vuông ABD = tam giác vuông ACD
=> DB = DC
=> tam giác DBC cân tại D
mà M là trung điểm BC
=> DM là trung trực, trung tuyến, phân giác của tam giác cân DBC
=> góc BMD = 90 độ
Ta có góc AMB = 90 độ; góc BMD = 90 độ
=> góc AMB + góc BMD = 90 độ + 90 độ = 180 độ
=> 3 điểm A,M,D thẳng hàng
a) do tam giac abc can tai a (gt)
-> ab=ac(t/c)
-> goc b=goc c(t/c)
theo gt am la trung tuyen
->m la trung diem cua bc
->bm=cm=bc/2 (t/c)
xet tam giac bem va tam giac cem co:
goc bem=cem=90 do
goc b=goc c (cmt)
bm=cm (cmt)
-> tam giac bem = tam giac cem (ch-gn)
cau a cua co giao lan thieu
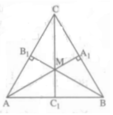

Gọi giao điểm của CM và AB là C1. Ta cần chứng minh CC1 ⊥ AB và C1 là trung điểm của đoạn thẳng AB. Vì trong một tam giác ba đường cao đồng quy nên CM hay CC1 vuông góc với AB.
+) Do tam giác ABC cân tại C có CM là đường cao nên CM đồng thời là đường trung trực của đoạn thẳng AB ( tính chất tam giác cân).