Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔHBC và ΔKCB có
HC=KB
\(\widehat{HCB}=\widehat{KBC}\)
BC chung
Do đó: ΔHBC=ΔKCB
Suy ra: \(\widehat{HBC}=\widehat{KCB}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O

2 cách
Cách 1
Do tam giác ABC cân tại A nên góc ABC=góc ACB và AB=AC
Do AB=AC mà AK=AH=> KB=HC
Xét tam giác BKC và tam giác CHB có:
-BK=HC -góc ABC=góc ACB -BC chung
=> tam giác BHC=tam giác CKB(c.g.c)
=>góc CHB=góc BKC
Xét tam giác KOB và tam giác HOC
-góc BKO=góc CHO
-BK=HK
-góc KOB=góc HOC
=>.tam giác KOB=tam giác HOC (g.c.g)
=>BO=CO ( chôc này bn có thể nói góc bằng nhau rồi cộng góc lại cx đc)
=> tam giác BOC cân tại O ( đpcm)
Cách 2
Xét tam giác ABH và tam giác ACK có
-AK=AH
-góc A chung
-AB=AC( tam giác ABC cân tại A)
=>góc ABH=góc ACB
=>góc HBC=góc KCB
=> tam giác OBC cân tại O ( Đpcm)

Xét tam giác ABH và ACK có:
AH=AK(gt)
AB=AC(tam giác ABC cân)
Â:góc chung
=> ABH=ACK
=> Góc ABH= Góc ACK
=> Góc OBC= Góc OCB
=> OBC cân tại O
Ta có tam giác ABC là tam giác cân tại A AB=AC; B=C (tính chất tam giác cân) Xét tam giác ACK và tam giác ABH có: AK=AH(giả thiết) A chung AC=AB(giả thiết) => tam giác ACK=tam giác ABH(c.g.c) OBC=OCB(2 góc tương ứng) Ta có B=OBC + KBO C=OCB + HCO Mà B=C(giả thiết) KBO= HCO(cmt) => OBC= OCB => OBC là tam giác cân

+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
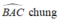
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.
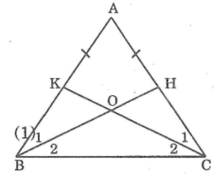

Hình vẽ:
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)