Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có tam giac ABC cân=>góc B=góc C . BÉ//D=>góc EBD= góc D1( so le trong ). Mà góc D=gốc FDC( đối đỉnh) <=>góc EBD=góc FDC .Mà góc B = góc C . Nên góc C=góc FDC. tam giác FCD cân tại F
tam giác EBD nè : ta có góc BED=góc EDF( so le trong) , góc CFD= góc EDF (so le trong ) <=> góc BED= góc EDF Nên: góc BED= góc CFD. và góc B= góc C . Nên góc EDB=góc FDC ( đ/l trong 1 tam giác ).Mà góc FDC=góc B. Nên góc B=góc EDB. Vậy tam giác EBD cân tại E

Vì DF // BA
\(\Rightarrow\widehat{FCD}=\widehat{EDB}\) (đồng vị)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{EBD}=\widehat{FCD}\)
\(\Rightarrow\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta EBD\) cân tại E
Vì ED // AC
\(\Rightarrow\widehat{EBD}=\widehat{FDC}\) (đồng vị)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{EBD}=\widehat{FCD}\)
\(\Rightarrow\widehat{FCD}=\widehat{FDC}\)
\(\Rightarrow\Delta FCD\) cân tại F
![]()

Ta có:
DE // AB (gt).
=> Góc B = Góc DEC (2 góc ở vị trí đồng vị).
Mà Góc B = Góc C (Tam giác ABC cân tại A).
=> Góc DEC = Góc C.
=> Tam DEC là tam giác cân tại D.

b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)

a) Xét ΔABC có
D∈AB(gt)
E∈AC(gt)
Do đó: \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(Hệ quả của Định lí Ta lét)
⇒\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
mà \(\dfrac{AB}{AC}=1\)(AB=AC)
nên \(\dfrac{AD}{AE}=1\)
hay AD=AE
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)

a: Xét tứ giác BDEM có
DE//BM
BD//EM
Do đó: BDEM là hình bình hành
Suy ra: DE=BM
mà DE=BC/2
nên BM=BC/2
hay M là trung điểm của BC
Xét ΔADE và ΔEMC có
\(\widehat{A}=\widehat{CEM}\)
DE=MC
\(\widehat{ADE}=\widehat{EMC}\)
Do đó: ΔADE=ΔEMC
b: Xét ΔABC có
DE//BC
nên AD/AB=DE/BC
=>AD/AB=1/2
=>AD=1/2AB
hay D là trung điểm của AB

gggggjjjk..hhhyh iuugln............................lklhuluiiiihhhhhhh ok-
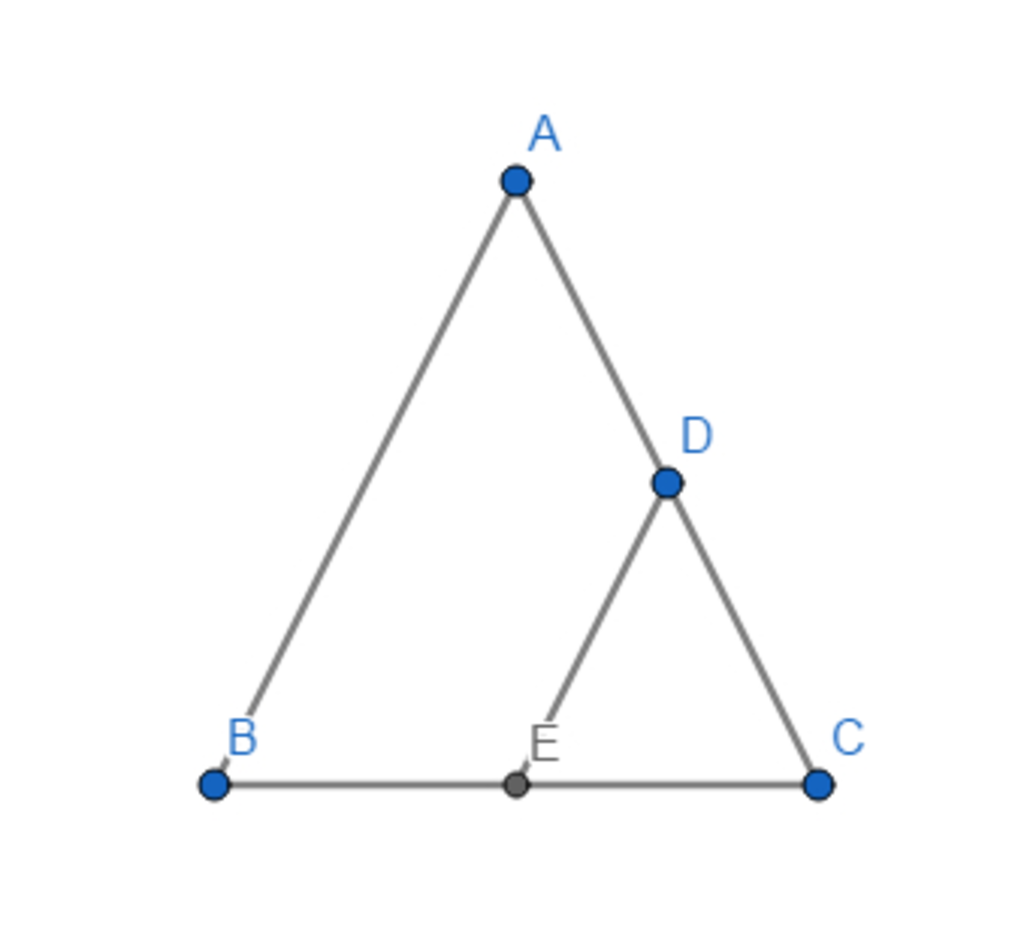
Xét ΔEBD có \(\widehat{EBD}=\widehat{EDB}\)
nên ΔEBD cân tại E
Xét ΔFCD có \(\widehat{FCD}=\widehat{FDC}\)
nên ΔFCD cân tại F