Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
6 tháng 2 2017 lúc 14:19
Cho tam giác ABC cân tại A , góc A=20 độ , vẽ tam giác đều DBC , D nằm trong tam giác ABC . Tia phân giác của góc ABD cắt AC tại H . Chứng minh :
a) Tia AD là tia phân giác của góc BAC
b) AM = BC
Hình thì chắc bạn vẽ được nên tớ không vẽ nữa!!!![]()
![]()
![]()
a, Đi chứng minh tam giác ABD=tam giác ACD (c.c.c) =>góc BAD=góc CAD=>AD là tia phân giác của góc BAC(đpcm)
nếu có j thắc mắc hỏi mình nha!!!![]()
![]()
b, tớ sửa đề chứng minh AH=BC do không có điểm M.
Chứng minh
Xét tam giác ABC cân tại A ta có:
góc ABC=góc ACB=(180độ -20 độ):2=160 độ:2=80độ (theo tính chất của tam giác cân)
ta lại có: góc DBC=60 độ( theo tính chất của tam giác đều)
mà góc ABD=góc ABC-góc DBC=80độ -60 độ=20độ
mặt khác góc BAD=gócCAD=20độ/2=10độ và góc ABD=20độ/2=10độ (theo tính chất của tia phân giác)
Xét tam giác ABH và tam giác BAD ta có:
góc BAH=góc ABD (=20độ); AB: cạnh chung; góc ABH=góc BAD(=10độ)
Do đó tam giác ABH = tam giác BAD
=> AH=BD mà BD=BC( theo tính chất của tam giác đều) nên AH=BC (đpcm)
Có chỗ nào vướng mắc hỏi mình nha!! Chúc bạn học giỏi!!![]()
![]()

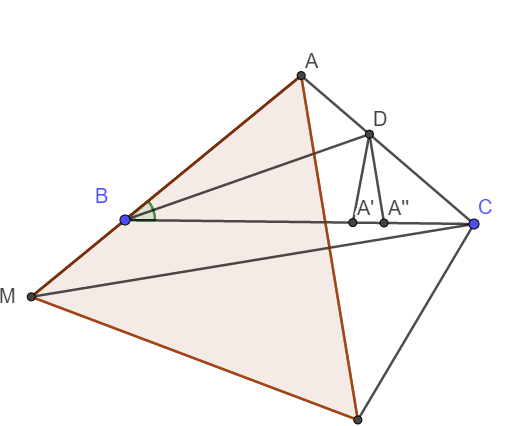
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA; BA'' = BD
Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\)
\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)
\(\Rightarrow\widehat{DA'A''}=80^o\)
Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)
Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)
Nên DA'' = CA''
Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD
b) Vẽ tam giác đều AMF.
Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)
Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)
\(\Rightarrow AC=CF\)
Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.
Vậy nên \(\widehat{MAC}=30^o\)

a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
c: Ta có: M nằm trên đường trung trực của AC
nên MA=MC
hay ΔMAC cân tại M