Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đó sẽ là hình thang cân DECB.
Trong bài tập này có 2 điều bạn phải làm rõ được:
DE // BC và DC = BE.
Chúng ta sẽ cùng làm từng điều một:
- DE // BC:
Giả thiết cho tam giác ABC cân A => AC = AB.
- Xét 2 tam giác ADE và ACB bằng nhau theo trường hợp cgc
=> góc ADE = ACB => DE // BC.
Còn phần còn lại bạn tự làm

(Bạn thông cảm nha. Mình vẽ hình không đẹp lắm)
Ta có \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)(\(\Delta ABC\)cân tại A) (1)
và AD = AE (gt)
nên \(\Delta ADE\)cân tại A
=> \(\widehat{AED}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2)
=> \(\widehat{ABC}=\widehat{AED}\)ở vị trí đồng vị (3)
=> BC // ED
nên tứ giác DEBC là hình thang (*)
Chứng minh tương tự, ta cũng có: \(\widehat{ACB}=\widehat{ADE}\)(4)
và \(\widehat{ABC}=\widehat{ACB}\)(\(\Delta ABC\)cân tại A) (5)
Từ (3), (4) và (5) => \(\widehat{AED}=\widehat{ADE}\)(**)
Từ (*) và (**)
=> Tứ giác DEBC là hình thang cân

Xét tứ giác BCDE có
A là trung điểm của EC
A là trung điểm của BD
Do đó: BCDE là hình bình hành
mà \(\widehat{EDC}=90^0\)
nên BCDE là hình chữ nhật

a: Xét ΔAED và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AD}{AB}\)
\(\widehat{EAD}=\widehat{CAB}\)
Do đó: ΔAED\(\sim\)ΔACB
Suy ra: \(\widehat{AED}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà EC=BD
nên BEDC là hình thang cân

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật

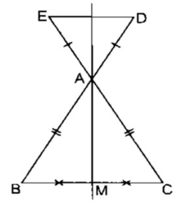
ΔABC cân tại A có AM là đường trung tuyến
⇒ AM là tia phân giác của góc (BAC)
⇒ ∠ (BAM) = ∠ (MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠ (BAM) = ∠ (DAN) (đối đỉnh) (2)
∠ (MAC) = ∠ (NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠ (DAN) = ∠ (NAE)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.
Đó sẽ là hình thang cân DECB.
Trong bài tập này có 2 điều bạn phải làm rõ được:
DE // BC và DC = BE.
Chúng ta sẽ cùng làm từng điều một:
- DE // BC:
Giả thiết cho tam giác ABC cân A => AC = AB.
- Xét 2 tam giác ADE và ACB bằng nhau theo trường hợp cgc
=> góc ADE = ACB => DE // BC.
học tốt nhé cậu
chép từ người khác à