Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét tam giác DBC và tam giác ECB có:
DB=EC (AB=AC và AD=AE)
góc ABC = góc ACB (cân tại A)
BC là cạnh chung
Do đó tam giác DBC = tam giác ECB (c.g.c)
Suy ra BE= CD (ĐPCM)

a/ Xét tam giác ABE và tam giác ADC có:
Góc A chung
AD=AE(gt)
AB=AC(gt)
=>Tam giác ABE=Tam giác ADC (c.g.c)
->BE=CD( 2 cạnh tương ứng)
b/Ta có:Tam giác ABC có AB=AC-> tam giác ABC cân tại A
Tam giác ABE=tam giác ADC (cmt)
-> Góc DBM= góc ECM (2 góc tương ứng) (1)
mà góc B=góc C ( tam giác ABC cân tại A)
-> Góc MBC=góc MCB
-> Tam giác MBC cân tại M
-> BM=CM(tính chất) (2)
Lại có: AB=AC; AD=AE
=> BD=EC (3)
Từ (1); (2) và (3) suy ra: tam giác BMD=tam giác CME(c.g.c)
c/Xét tam giác ABM và tam giác ACM có:
AB=AC(gt)
Góc ABM= góc ACM(CMt)
BM=CM(cmt)
=> Tam giác ABM=Tam giác ACK (c.g.c)
-> góc BAM=góc CAM(2 góc tương ứng)
hay AM là phân giác góc BAC
a, Xét tam giác ABE và tam giác ACD có
^A _ chung ; AB = AC ; AE = AD
Vậy tam giác ABE = tam giác ACD (c.g.c)
=> BD = CD ( 2 cạnh tương ứng )
b, Xét tam giác BMD và tam giác CME
BD = CE ; ^BMD = ^CME ( đối đỉnh ) ; BD = CE
do AB = AC và AD = AE
Vậy tam giác BMD = tam giác CME (c.g.c)

a: Xét ΔAEBvà ΔADC có
AE=AD
góc A chung
AB=AC
=>ΔAEB=ΔADC
=>BE=CD
b: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
c: Xét ΔAMB và ΔAMC có
MA chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
`@`` \text {dnv}`
`a,`
Xét `\Delta ABE` và `\Delta ACD`:
`\text {AB = AC (Tam giác ABC cân tại A)}`
`\hat {A}`` \text {chung}`
`\text {AD = AE (gt)}`
`=> \Delta ABE = \Delta ACD (c-g-c)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Vì `\Delta ABE = \Delta ACD (a)`
$ -> \widehat {ACD} = \widehat {ABE} (\text {2 góc tương ứng})$
`->` $\widehat {ADC} = \widehat {AEB} (\text {2 góc tương ứng})$
Ta có: \(\left\{{}\begin{matrix}\widehat{ADC}+\widehat{BDC}=180^0\\\widehat{AEB}+\widehat{CEB}=180^0\end{matrix}\right.\)
$\widehat {ADC} = \widehat {AEB}$
`->` $\widehat {CEB} = \widehat {BDC}$
Ta có:\(\left\{{}\begin{matrix}\text{AB = AD + DB}\\\text{AC = AE + EC}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{AD = AE}\end{matrix}\right.\)
`-> \text {BD = EC}`
Xét `\Delta BMD` và `\Delta CME`:
\(\widehat{\text{DBM}}=\widehat{\text{ECM}}\left(\text{CMT}\right)\)
\(\text{BD = CE (CMT)}\)
\(\widehat{\text{BDM}}=\widehat{\text{CEM}\text{ }}\text{ }\left(\text{CMT}\right)\)
`=> \Delta BMD = \Delta CME (g-c-g)`
`c,` Đề có phải là "Chứng minh AM là phân giác của góc BAC" ?
Vì `\Delta BMD = \Delta CME (b)`
`-> \text {MB = MC (2 cạnh tương ứng)}`
Xét `\Delta BAM` và `\Delta CAM`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\text {AM chung}`
`\text {MB = MC (CMT)}`
`=> \Delta BAM = \Delta CAM (c-c-c)`
`->` $\widehat {BAM} = \widehat {CAM} (\text {2 góc tương ứng})$
`-> `\(\text{AM là tia phân giác của }\widehat{\text{BAC}}\)
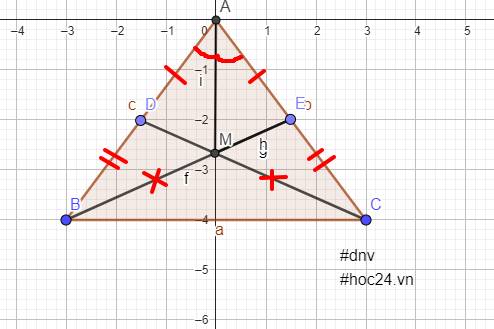

Xét tam giác ABE và tam giác ACD có
AB=AC(gt)
AD=AE(gt)
góc A chung
\(\Rightarrow\)tam giác ABE= tam giác ACD(cgc)
\(\Rightarrow\)BE=CD(2 cạnh tương ứng)

Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)
Bài giải
* Hình tự vẽ
a) Xét tam giác AEB và tam giác ADC có:
Góc A là góc chung
AD = AE (gt)
AB = AC ( tam giác ABC cân tại A )
-> Tam giác AEB = tam giác ADC (c-g-c)
-> BE = CD (hai cạnh tương ứng)
a) Tam giác ABC cân tại A nên AB = AC .
Xét hai tam giác ABE và ACD có: AB = AC, góc A chung và AE = AD nên tam giác ABE = tam giác ACD.
=> BE = CD
P/s: b) , c) bn tự lm nhé, xin lỗi!