Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABM và tam giác ACN:
Góc A chung
AB = AC (do tam giác ABC cân tại A)
AM = AN (gt)
Suy ra: tam giác ABM = tam giác ACN (c g c)
b) Xét tam giác AMN có :
AM =AN (gt)
Suy ra: tam giác AMN cân tại A
Suy ra góc ANM = \(\dfrac{\text{180 - góc A}}{2}\)
mà góc ABC = \(\dfrac{\text{180 - góc A}}{2}\) ( do tam giác ABC cân tại A)
Suy ra: góc ANM = góc ABC
Mà 2 góc này ở vị trí đồng vị của MN và BC
Suy ra MN song song BC

a. xét tam giác ABH và tam giác ACH
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
BH = CH ( ABC cân, AH là đường cao cũng là trung tuyến )
Vậy tam giác ABH = tam giác ACH ( c.g.c )
b. xét tam giác vuông BNH và tam giác vuông CNH
BN = CM ( AB = AC ; AM = AN )
BH = CH
Vậy tam giác vuông BNH = tam giác vuông CNH ( cạnh huyền. cạnh góc vuông )
c. áp dụng định lý pitao vào tam giác vuông AHB:
\(AB^2=AH^2+BH^2\)
\(BH=\sqrt{10^2-8^2}=\sqrt{64}=8cm\)
=> BC = BH. 2 = 8.2 =16 cm
Chúc bạn học tốt!!!
a, Xét tam giác ABH và tam giác ACH
^AHB = ^AHC = 900
AB = AC (gt)
AH _ chung
Vậy tam giác ABH = tam giác ACH ( ch - cgv )
b, Xét tam ANB và tam giác AMC có :
^A _ chung
AM = AN(gt)
AB = AC (gt)
Vậy tam giác ANB = tam giác AMC ( c.g.c )
=> BN = CM ( 2 cạnh tương ứng )
c, Xét tam giác ABH vuông tại H, theo định lí Pytago
\(BH=\sqrt{AB^2-AH^2}=6cm\)
Xét tam giác ABC cân tại A có AH là đường cao nên đồng thời AH là đường trung tuyến
=> BC = 2BH = 12 cm

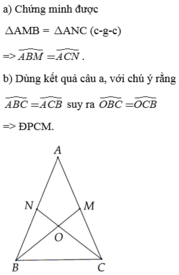
a: Xét ΔMBC và ΔNCB có
MB=NC
\(\widehat{MBC}=\widehat{NCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔMBC=ΔNCB
b: ΔMBC=ΔNCB
=>\(\widehat{MCB}=\widehat{NBC}\)
Ta có: \(\widehat{ABN}+\widehat{CBN}=\widehat{ABC}\)
\(\widehat{ACM}+\widehat{MCB}=\widehat{ACB}\)
mà \(\widehat{ABC}=\widehat{ACB};\widehat{CBN}=\widehat{MCB}\)
nên \(\widehat{ABN}=\widehat{ACM}\)
c: AM+MB=AB
AN+NC=AC
mà AB=AC
và MB=NC
nên AM=AN
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
d: Ta có: \(\widehat{MCB}=\widehat{NBC}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
AB=AC
=>A nằm trên đường trung trực của BC(2)
IB=IC
=>I nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng

a: AM+MC=AC
NA+NB=AB
mà AB=AC; AM=AN
nên MC=NB
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc OBC=góc OCB
=>ΔOBC cân tại O