Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Ta có: ΔABC cân tại A(gt)
mà AM là đường phân giác ứng với cạnh đáy BC(gt)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
\(\Leftrightarrow AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(cmt)
BK là đường cao ứng với cạnh AC(Gt)
AM cắt BK tại I(Gt)
Do đó: I là trực tâm của ΔBAC(Tính chất ba đường cao của tam giác)
Suy ra: CI\(\perp\)AB(Đpcm)

a) Tam giác ABC cân tại A có AM là phân giác, do đó AM cũng là đường cao
AM vuông góc với BC
Lại có BK vuông góc với AC
Do đó I là trực tâm của tam giác ABC
Vậy CI vuông góc với AB
b) Tam giác BDH = tam giác DBP (ch.gn)
Do đó BH = DP
BDKQ là hình chữ nhật => DP = HK
=> BK = BH + HK = DP + DQ (đpcm)

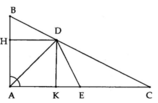

c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAHC
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC
c; AK=8cm nên AH=8cm
AI=căn 8^2+6^2=10cm

a: Xet ΔADB và ΔADE có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: Xét ΔAHD vuông tại HvàΔAKD vuông tại K co
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
=>DH=DK
=>D cách đều AB,AC

a: Xét ΔABC có
AM,BK là đường cao
AM cắt BK tại I
=>I là trực tâm
=>CI vuông góc AB tại N
b:
Xet ΔAKB vuông tại K và ΔANC vuông tại N có
AB=AC
góc KAB chung
=>ΔAKB=ΔANC
=>BK=CN
DP//NC
=>DP/NC=BD/BC
=>DP/BK=BD/BC
DQ//BK
=>DQ/BK=CD/CB
=>DQ+DP=BK(BD/BC+CD/CB)=BK

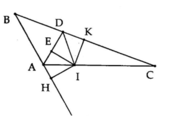
⇒ ∠KAH = ∠MAH
Xét hai tam giác vuông: ∆KAH và ∆MAH có:
AH là cạnh chung
∠KAH = ∠MAH (cmt)
⇒ ∆KAH = ∆MAH (cạnh huyền - góc nhọn)
b) Do ∆KAH = ∆MAH (cmt)
⇒ AK = AM (hai cạnh tương ứng)
∆AKM có:
AK = AM (cmt)
⇒ ∆AKM cân tại A
⇒ ∠AKM = ∠AMK = (180⁰ - ∠KAM) : 2
= (180⁰ - ∠BAC) : 2 (1)
∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (2)
Từ (1) và (2) ⇒ ∠AKM = ∠ABC
Mà ∠AKM và ∠ABC là hai góc đồng vị
⇒ KM // BC