Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh BC
nên AH là đường trung tuyến ứng với cạnh BC
Ta có: AB=AC
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(3)
Từ (1), \(\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
\(\Leftrightarrow A,O,H,D\) thẳng hàng
hay AD là đường kính của \(\left(O\right)\)

a/ vì (o) ngoại tiếp tam giác ABC => o là giao điểm 3 đường cao
mà tam giác ABC cân tại A => đường cao AH đồng thời là trung trực của BC
=>O thuộc AH
lại có AH giao (o) tại D => AD là đường kính

a) Ta có: ΔABC cân tại A(gt)
mà AH là đường cao ứng với cạnh đáy BC(gt)
nên H là trung điểm của BC
Ta có: AB=AC(ΔABC cân tại A
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
hay A,O,H,D thẳng hàng
hay AD là đường kính của \(\left(O\right)\)
Xét \(\left(O\right)\) có \(\widehat{ACD}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACD}=90^0\)

c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5
a) ta có DOC=cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC=2*AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
từ (1);(2) ta dc DOC+AOC=180
b)góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) đợi xí

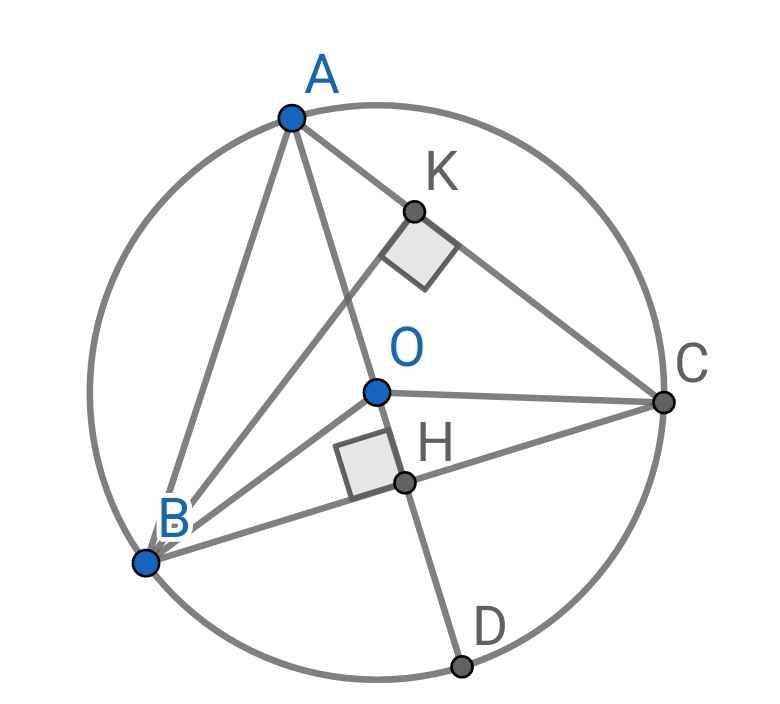 a) Ta có:
a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)

a, Tam giác ABC cân tại A nên AH là đường trung trực của BC. Do đó AD là đường trung trực của BC. Vì O nằm trên đường trung trực của BC nên O nằm trên AD. Vậy AD là đường kính của đường tròn (O).
b, Tam giác ACD nội tiếp đường tròn đường kính AD nên ∠ACD = 90o
c, Ta có BH = HC = BC/2 = 12(cm)
Tam giác AHC vuông tại H nên AH2 = AC2 - HC2 = 202 - 122 = 256
=> AH = 16(cm)
AC2 = AD. AH
AD = AC2/AH = 25(cm)
Bán kính đường tròn(O) bằng 12,5cm.
a, Tam giác ABC cân tại A nên AH là đường trung trực của BC. Do đó AD là đường trung trực của BC. Vì O nằm trên đường trung trực của BC nên O nằm trên AD. Vậy AD là đường kính của đường tròn (O).
b, Tam giác ACD nội tiếp đường tròn đường kính AD nên ∠ACD = 90o
c, Ta có BH = HC = BC/2 = 12(cm)
Tam giác AHC vuông tại H nên AH2 = AC2 - HC2 = 202 - 122 = 256
=> AH = 16(cm)
AC2 = AD. AH
AD = AC2/AH = 25(cm)
Bán kính 25 cm