Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABC\) cân tại A:
AI là đường cao (AI vuông góc BC, I thuộc BC).
\(\Rightarrow\) AI là đường trung tuyến (T/c \(\Delta\) cân).
\(\Rightarrow\) I là trung điểm BC.
Vì \(\Delta ABC\) cân tại A (gt).
\(\Rightarrow AB=AC;\widehat{B}=\widehat{C}\) (T/c \(\Delta\) cân).
Ta có: \(EB=AB-AE;FC=AC-AF.\)
Mà \(\left\{{}\begin{matrix}AE=AF\left(gt\right).\\AB=AC\left(cmt\right).\end{matrix}\right.\)
\(\Rightarrow EB=FC.\)
Xét \(\Delta EBI\) và \(\Delta FCI:\)
\(EB=FC\left(cmt\right).\\ \widehat{B}=\widehat{C}\left(cmt\right).\)
\(IB=IC\) (I là trung điểm BC).
\(\Rightarrow\Delta EBI\) \(=\Delta FCI\left(c-g-c\right).\)
\(\Rightarrow IE=IF\) (2 cạnh tương ứng).
\(\Rightarrow\Delta IEF\) cân tại I.

Sửa đề: AI vuông góc với BC
a) Xét ΔAIB vuông tại I và ΔAIC vuông tại I có
AB=AC(ΔABC cân tại A)
AI chung
Do đó: ΔAIB=ΔAIC(cạnh huyền-cạnh góc vuông)
Suy ra: IB=IC(hai cạnh tương ứng)
mà B,I,C thẳng hàng(gt)
nên I là trung điểm của BC(đpcm)
b) Ta có: ΔAIB=ΔAIC(cmt)
nên \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)
hay \(\widehat{EAI}=\widehat{FAI}\)
Xét ΔEAI và ΔFAI có
AE=AF(gt)
\(\widehat{EAI}=\widehat{FAI}\)(cmt)
AI chung
Do đó: ΔEAI=ΔFAI(c-g-c)
Suy ra: IE=IF(hai cạnh tương ứng)
Xét ΔIEF có IE=IF(cmt)
nên ΔIEF cân tại I(Định nghĩa tam giác cân)
c) Ta có: AE+EB=AB(E nằm giữa A và B)
AF+FC=AC(F nằm giữa A và C)
mà AE=AF(gt)
và AB=AC(ΔABC cân tại A)
nên EB=FC
Xét ΔEBI và ΔFCI có
EB=FC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
BI=CI(cmt)
Do đó: ΔEBI=ΔFCI(c-g-c)

Chứng minh câu a
Xét tam giác ABI và tam giác ACI có:
AI cạnh chung
AB = AC ( tam giác ABC cân tại A )
Suy ra tam giác ABI = tam giác ACI ( c-g-c )
Suy ra BI = CI

a: Ta có: ΔABC cân tại A
mà AI là đường cao
nên I là trung điểm của BC
b: Ta có: ΔABC cân tại A
mà AI là đường cao
nên AI là đường phân giác
Xét ΔEAI và ΔFAI có
AE=AF
\(\widehat{EAI}=\widehat{FAI}\)
AI chung
DO đó: ΔEAI=ΔFAI
Suy ra: IE=IF
hay ΔIEF cân tại I
c: Xét ΔEBI và ΔFCI có
EB=FC
BI=CI
IE=IF
Do đó: ΔEBI=ΔFCI

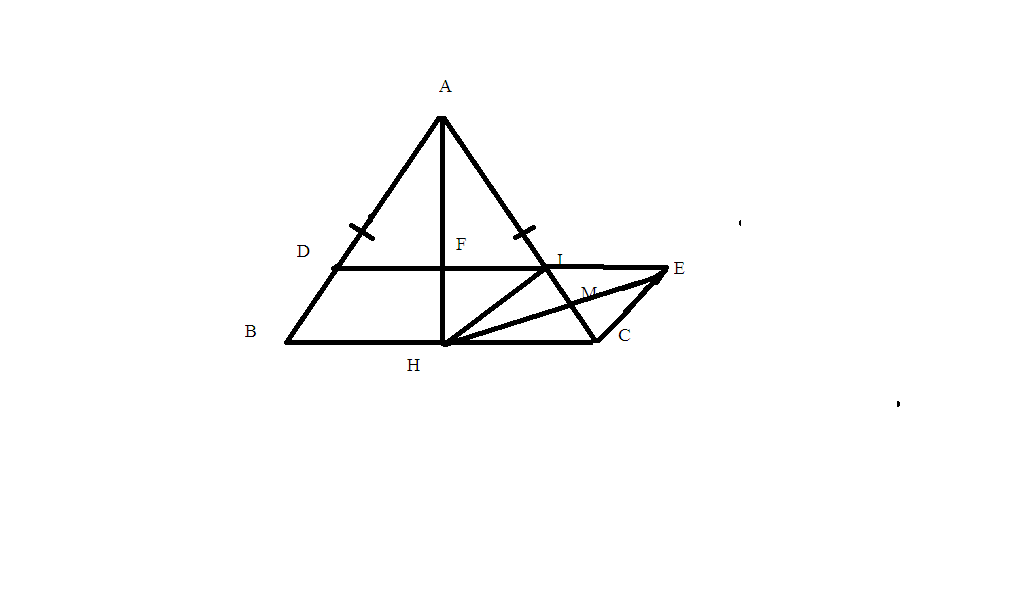
a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI
a) Vi tam giac ABC can tai A => B=C va AB = AC( t/c tam giac can )
Xet tam giac AIB va tam giac AIC co
AB=AC(gt)
B=C(gt)
=> tam giac AIB=AIC(canh huyen goc - goc nhon)
=> BI=IC ( 2 goc tuong ung)
vay I la trung diem cua BC