Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC(Cạnh huyền-góc nhọn)
b. Ta có : AB = BE + EA
CA = CD + DA
MÀ : AB=CA ( TAM GIÁC ABC CÂN TẠI A )
EA=DA ( ΔADB=ΔAEC)
⇒BE=CD
XÉT ΔOBE VÀ ΔOCD
CÓ : \(\widehat{E}=\widehat{D}\) (GT)
BE=CD (CMT)
\(\widehat{EBO}=\widehat{DCO}\) (ΔADB=ΔAEC)
⇒ΔOBE = ΔOCD (G-C-G)
⇒OB = OC (2 CẠNH TƯƠNG ỨNG)
⇒ΔBOC CÂN TẠI O

a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó:ΔABD=ΔACE
Suy ra: AD=AE
c: Ta có: ΔBEC=ΔCDB
nên \(\widehat{IBC}=\widehat{ICB}\)
hayΔIBC cân tại I
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó:ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
d: Xét ΔABC có AE/AB=AD/AC
nên DE//BC

a: Xét ΔADB vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔACE
b: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I

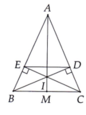


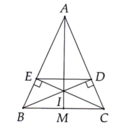
help me
a) Xét tam giác vuông ADB và tam giác vuông ACE có:
Góc A chung
AB = AC (gt)
\(\Rightarrow\Delta ABD=\Delta ACE\) (Cạnh huyền - góc nhọn)
b) Do \(\Delta ABD=\Delta ACE\Rightarrow AD=AE\)
Xét tam giác vuông AEH và tam giác vuông ADH có:
Cạnh AH chung
AE = AD (cmt)
\(\Rightarrow\Delta AEH=\Delta ADH\) (Cạnh huyền - cạnh góc vuông)
\(\Rightarrow HE=HD\)
c) Xét tam giác ABC có BD, CE là đường cao nên chúng đồng quy tại trực tâm. Vậy H là trực tâm giác giác.
Lại có AM cũng là đường cao nên AM đi qua H.
d) Xét các tam giác vuông EBC và EAC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=EB^2+EA^2;AC^2=EA^2+EC^2\)
Tam giác ABC cân tại A nên AB = AC hay \(AB^2=AC^2\)
Vậy nên \(AB^2+AC^2+BC^2=2AC^2+BC^2=2\left(EA^2+EC^2\right)+EB^2+EC^2\)
\(=3EC^2+2EA^2+BC^2\).