Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC cân tại A
mà AE là phân giác
nên AE là trung trực của BC
b: O nằm trên trung trực của AB
=>OA=OB
O nằm trên trung trực của BC
=>OB=OC
=>OA=OC
=>O nằm trên trung trực của AC
c: OA=OB=OC
=>O cách đều 3 đỉnh của ΔABC

bài 2:
ta có : điểm M nằm trên đường trung trực của BC nên M sẽ cách đều B và C => MB=MC
Ta có: AC=AM+MC
=> AC=AM+MB
Bài 2: Tam giác BNC cân tại N vì đường thẳng hạ từ N xuống vuong góc cạnh đối diện cũng là trung tuyến nên BN=NC
=> AN+BN=AN+NC=AC

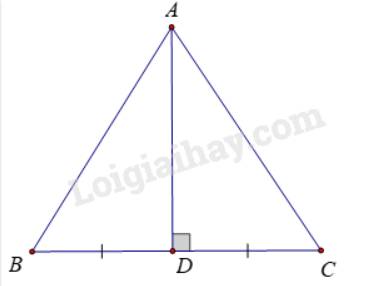
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
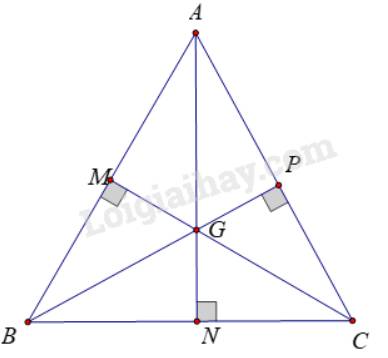
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất

a: Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
=>góc MAO=góc NAO
=>AO là phân giác của góc MAN
b: OB=OA
OA=OC
Do đó: OB=OC
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC

a) XÉT \(\Delta BAD\)VÀ \(\Delta MAD\)CÓ
\(\widehat{ABD}=\widehat{AMD}=90^o\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AD LÀ CẠNH CHUNG
=>\(\Delta BAD\)=\(\Delta MAD\)( CH-GN)
B) VÌ \(\Delta BAD\)=\(\Delta MAD\)(CMT)
\(\Rightarrow BA=MA\)HAI CẠNH TƯƠNG ỨNG
\(\Rightarrow\Delta ABM\) CÂN TẠI A
MÀ \(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
=> AI LÀ PHÂN GIÁC CỦA \(\widehat{BAM}\)
MÀ TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG TRUNG TRỰC
=> AI LÀ ĐƯỜNG TRUNG TRỰC CỦA ĐỌAN BM
MÀ I NẰM TRÊN ĐỌAN AD
=> AD LÀ ĐƯỜNG TRUNG TRỰC CỦA ĐỌAN BM
C)
chứng minh DH=DB=DM
sao đó là mà D là điểm nằm trog tam giác acn
=> d cách đều các cạnh tam giác acn

a) Xét ΔABO vuông tại O và ΔAEO vuông tại O có
AO chung
\(\widehat{BAO}=\widehat{EAO}\)(AO là tia phân giác của \(\widehat{BAE}\))
Do đó: ΔABO=ΔAEO(cạnh góc vuông-góc nhọn kề)
b) Ta có: ΔABO=ΔAEO(cmt)
nên AB=AE(Hai cạnh tương ứng)
Xét ΔABE có AB=AE(cmt)
nên ΔABE cân tại A(Định nghĩa tam giác cân)



vẽ hình ta thấy 0 là trục tâm vì là giao điiẻm của 2 đường cao nên o cách đều 3 đỉnh