Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

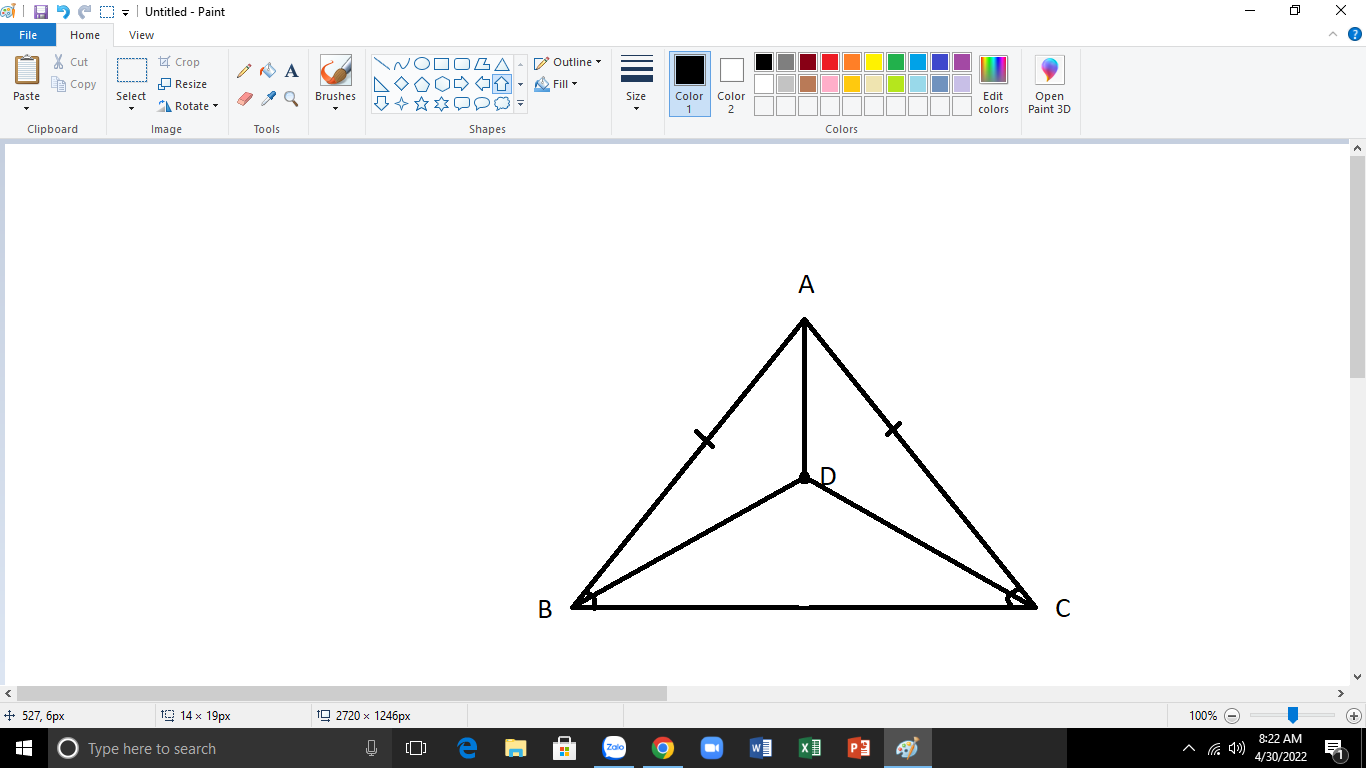
\(\text{a)Xét }\Delta ABD\text{ và }\Delta ACD\text{ có:}\)
\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
\(AD\text{ chung}\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\left(\text{hai góc tương ứng}\right)\)
\(\text{b)Ta có:}\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)
\(\text{Mà }\widehat{ABD}=\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)

Đây nha:
a. Xét tam giác ABD và tam giác ACD có:
góc BAD = góc BAC (gt)
AD chung
AB = AC (tam giác ABC cân)
=> tam giác ABD = tam giác ACD (cgc)
b. Gọi E là trung điểm của BC
Có: góc BAC = góc BAD + góc CAD mà góc BAD = góc CAD
=> AD là đường phân giác
Lại có: tam giác ABC cân tại A => AD đồng thời là đường trung trực của tam giác ABC
Do đó: DE là đường trung trực cũng là đường phân giác của tam giác BDC.
=> DE vuông với BC tại E; góc BDE = góc CDE
Xét tam giác BDE và tam giác CDE vuông tại E có:
DE chung
góc BDE = góc CDE (cmt)
=> tam giác BDE = tam giác CDE (ch-cgv)
=> góc DBC = góc DCB (2 góc tương ứng)

http://d.violet.vn//uploads/resources/285/2783442/preview.swf
trang 73

a) Xét tam giác ADB và ADC có: AD chung
DB=DC(vì tam giác DBC đều)
AB=AC ( tam giác ABC cân tại A)
=> tam giác ADB=tam giác ADC (c.c.c)
=>\(\widehat{ADB}=\widehat{ADC}\)(2 góc tương ứng)
mà AD nằm giữa AB và AC
=>AD là tia p/g của góc BAC
b. Ta có: ΔABC cân tại A, mà = 200 (gt)
=> = (1800 - 200) : 2 = 800
ΔABC đều nên = 600
Tia BD nằm giữa hai tia BA và BC
=> = 800 - 600 = 200
Tia BM là tia phân giác của góc ABD
=> = 100
Xét ΔABM và ΔBAD ta có:
\(\widehat{ABM}=\widehat{DAB}=10^0\)
AB là cạnh chung
\(\widehat{BAM}=\widehat{ABD}=20^0\)
Vậy ΔABM = ΔBAD (g - c - g)
Suy ra AM = BD
mà BD = BC ( gt )
=> AM = BC

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD