Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ đường cao AH ; Vì \(\Delta\)ABC cân
=> H là trung điểm BC
Xét \(\Delta\)ABC cân tại A có ^A = 120\(^o\)
=> ^ABH = ^ACH = 30\(^o\)
=> ^BAH = 60 \(^o\)
Lấy A' đối xứng với A qua H; BH vuông góc AA'; H là trung điểm AA'
=> \(\Delta\)ABA' cân tại B mà ^BAA' = ^BAH = 60\(^o\)
=> \(\Delta\)ABA' đều .
Đặt: AB = x => AA' = x => AH = x/2
+) \(\Delta\)ABH vuông tại H => BH\(^2\)= AB\(^2\)- AH\(^2\)= \(x^2-\frac{x^2}{4}=\frac{3x^2}{4}\)
=> \(BH=\frac{\sqrt{3}x}{2}\)
=> \(BC=2BH=\sqrt{3}x=\sqrt{3}AB\)
( Như vậy chúng ta có nhận xét: Cho \(\Delta\)ABC cân tại A; ^A = 120\(^o\)=> \(BC=\sqrt{3}AB\))
=> \(AC=AB=\frac{BC}{\sqrt{3}}=\frac{6}{\sqrt{3}}\)
+) Xét \(\Delta\)ABD vuông tại A có: ^ABD = ^ABH = 30 \(^o\)=> ^ADB = 60\(^o\)
=> ^ADC = 180\(^o\)- ^ADB = 180\(^o\)- 60 \(^o\)= 120\(^o\)
Mà ^BAC = 120\(^o\); ^BAD = 90\(^o\)
=> ^DAC = 120\(^o\)- 90 \(^o\)= 30\(^o\)
+) Xét \(\Delta\)DAC có: ^DAC = 30\(^o\); ^ADC = 120\(^o\) => ^DCA = 30\(^o\)
=> \(\Delta\)DAC cân tại D và có: ^ADC = 120\(^o\). Theo nhận xét in đậm ở trên: \(AC=\sqrt{3}.DC\)
=> \(DC=\frac{AC}{\sqrt{3}}=\frac{\frac{6}{\sqrt{3}}}{\sqrt{3}}=\frac{6}{3}=2\)
=> \(BD=BC-DC=6-2=4cm\)

Ta có: BAC=120, BAD=90 => DAC=30
Vì tam giác ABC cân nên B=C
Trong tam giác ABC có
BAC + B + C=180(tổng 3 góc trong tam giác)
=> B + C=60
Mà: B=C =>: B= C=30
Trong tam giác ADC có: DAC=C nên tam giáccân tại \D
=> AD=CD
Vì tam giác ABD là nửa tam giác đều
=> AD= \(\frac{1}{2}\) BD
Mà BD=DC => DC=
21 BD
Ta có BD+DC=\(\frac{1}{2}\)BC
Mà DC=\(\frac{1}{2}\) BD
Thì ta dễ dàng suy ra được BD=4,còn DC=2
Vậy BD=4
p/s : kham khảo
Ta có: BAC=120, BAD=90 => DAC=30
Vì tam giác ABC cân nên B=C
Trong tam giác ABC có
BAC + B + C=180(tổng 3 góc trong tam giác)
=> B + C=60
Mà: B=C =>: B= C=30
Trong tam giác ADC có: DAC=C nên tam giáccân tại \D
=> AD=CD
Vì tam giác ABD là nửa tam giác đều
=> AD= 12 BD
Mà BD=DC => DC=
21 BD
Ta có BD+DC=12 BC
Mà DC=12 BD
Thì ta dễ dàng suy ra được BD=4,còn DC=2
Vậy BD=4

Ta có: BAC = 120 độ ; CAD = 90 độ => DAB = 30 độ.
Vì tam giác ABC cân nên B = C
Trong tam giác ABC có:
BAC + B + C = 180 độ(tổng 3 góc trong tam giác)
=> B + C= 60 độ
Mà: B = C => B = C = 30 độ
Trong tam giác ADC có: DAB = B =>Tam giác ADB là tam giác cân tại D => AD = BD.
Vì tam giác ACD vuông mà B = 30 => AD = \(\frac{1}{2}\)DC.
Mà: AD = BD => BD = \(\frac{1}{2}\)DC.
Ta lại có: BD + DC = BC => BD = \(\frac{1}{3}\)BC
=> BD = \(\frac{1}{3}\) x 6 = 2(cm)
Vậy BD = 2 cm
(Mình vì nếu viết kí hiệu góc thì rất lâu nên mình dùng luôn dấu gạch ngang trên đầu của góc nha bạn)

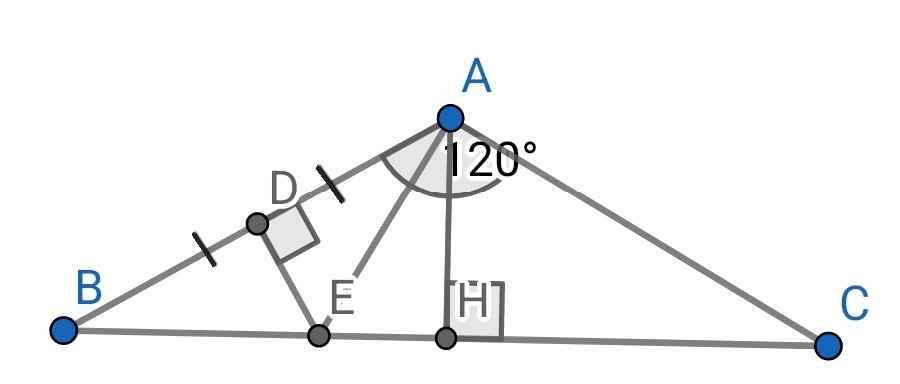 Do ∆ABC cân tại A (gt)
Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
∆AHB vuông tại H (do AH ⊥ BC)
⇒ ∠B + ∠BAH = 90⁰
⇒ ∠BAH = 90⁰ - ∠B
= 90⁰ - 30⁰
= 60⁰
Xét hai tam giác vuông: ∆AED và ∆BED có:
ED là cạnh chung
AD = BD (do D là trung điểm của AB)
⇒ ∆AED = ∆BED (hai cạnh góc vuông)
⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)
⇒ ∠EAH = ∠BAH - ∠EAD
= 60⁰ - 30⁰
= 30⁰
⇒ ∠EAH = ∠EAD
Xét hai tam giác vuông: ∆AEH và ∆AED có:
AE là cạnh chung
∠EAH = ∠EAD = 30⁰
⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)
Mà ∆AED = ∆BED (cmt)
⇒ ∆BED = ∆AEH


