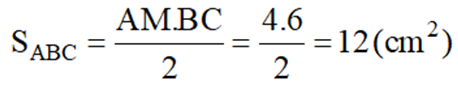Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=6cm
nên BM=CM=3cm
=>AM=4cm
\(S_{ABC}=\dfrac{3\cdot4}{2}=6\left(cm^2\right)\)
b: Xét tứ giác AMCK có
O là trung điểm của AC
O là trung điểm của MK
Do đó;AMCK là hình bình hành
Suy ra: AK//MC
c: Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật

a: ΔABC cân tại A
mà AM là phân giác
nên AM vuôg góc BC và M là trung điểm của BC
\(BM=CM=\dfrac{60}{2}=30\left(cm\right)\)
\(AM=\sqrt{50^2-30^2}=40\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot40\cdot60=20\cdot60=1200\left(cm^2\right)\)
b: Xét ΔOAK và ΔOCM có
OA=OC
góc AOK=góc COM
OK=OM
=>ΔOAK=ΔOCM
=>góc OAK=góc OCM
=>AK//CM
b: Xét tứ giác AMCK có
AK//CM
AK=CM
góc AMC=90 độ
=>AMCK là hfinh chữ nhật
d: Để AMCK là hình vuông thì AM=CM=BC/2
=>ΔABC vuông tại A

a) Vì \(\widehat{M}\) là trung điểm của \(\widehat{BC}\) nên:
\(\widehat{BM}=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
\(\Delta ABC\) cân tại \(A\), lại có \(\widehat{AM}\) là đường phân giác nên \(\widehat{AM}\) cũng là đường cao. Do đó \(\Delta AMB\) vuông tại \(\widehat{M}\)
\(\Rightarrow AM^2=AB^2-BM^2\) ( theo định lí Pytago )
\(\Rightarrow\widehat{AM}=4cm\)
\(S_{ABC}=\dfrac{AM.BC}{2}=\dfrac{4.6}{2}=12\left(cm^2\right)\)
b) \(\Delta AMC\) vuông tại\(M\) có \(\widehat{MO}\) là đường trung tuyến nên \(\widehat{OM}=\widehat{OA}\)
\(\Rightarrow\text{∠}OAM=\text{∠}OMA\)( \(\Delta AMO\) cân tại \(O\))
Lại có \(\text{∠}OAM=\text{∠}MAB\) ( \(AM\) là tia phân giác của \(BAC\) )
\(\Rightarrow\text{∠}OMA=\text{∠}MAB\)
Mà đây là 2 góc ở vị trí so le trong
\(\Rightarrow OM\text{ // }AB\)
Vậy tứ giác \(ABMO\) là hình thang.
c) Tứ giác \(AMCK\) có \(\widehat{OA}=\widehat{OC};\widehat{OM}=\widehat{OK}\) nên tứ giác \(AMCK\) là hình bình hành . Lại có \(\text{∠}AMC=90^o\)(chứng minh trên) nên tứ giác \(ACMK\) là hình chữ nhật
Hình chữ nhật \(ACMK\) là hình vuông
\(\Leftrightarrow\widehat{AM}=\widehat{MC}=\widehat{BM}\)
\(\Leftrightarrow\widehat{AM}=\dfrac{BC}{2}\)
\(\Leftrightarrow\Delta ABC\) vuông tại \(\widehat{A}\)
TK
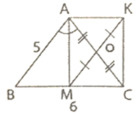
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.

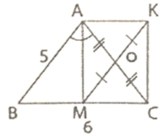
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
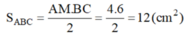
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.

a: AM=BC/2=3cm
b: Xét tứ giác AMCN có
O là trung điểm chung của AC và MN
MA=MC
Do đó: AMCN là hình thoi

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

b: Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
hay MN⊥AB