Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/Ta có : M là Trung điểm của AD
N là trung diểm của BC
\(\Rightarrow\)MN là dường trung bình của hình thang
Theo định lí dường trung bình của hình thang( học tới đó thì cm minh ngay)
Thì MN=(AB+CD)/2
b/k có câu nào cho cm như vậy hết

Giải
Ta thấy đường trung bình tam giác ABC nên BEDC là hình thang, lại có\(BM=MC\cdot DN=NC\Rightarrow MN\) là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì
\(MI=KN=\frac{DE}{2}\left(1\right)\)
\(MN=\frac{DE^2+BC}{2}\Rightarrow IK=MN-2MI=\frac{DE+BC}{2}-DE\)
\(=\frac{BC-DE}{2}=\frac{DE^2}{2}\left(BC=2DE\right)\left(2\right)\)
\(\Leftrightarrow Q\cdot E\cdot D\Rightarrowđcpm\)
![[IMG]](http://d.f10.photo.zdn.vn/upload/original/2012/07/09/20/02/1341838952939363106_574_0.jpg)
Mình sẽ làm câu b trước rồi từ đó suy ra a
b)Giả sử MP=PQ=QN đã có từ trước
Xét △△ ABC có E là trung điểm AB,D là trung điểm AC \Rightarrow ED là đường trung bình của △△ ABC\Rightarrow ED//BC và ED=BC/2(*)
Xét hình thang EDBC có M là trung điểm BE,N là trung điểm CE \Rightarrow MN//BC( (*) (*) )
Từ (*)( (*) (*) ) \Rightarrow ED//MN
Xét △△ BED có M là trung điểm BE,MP//ED \Rightarrow MP là đường trung bình của △△ BED \Rightarrow MP=ED/2
Tương tự cũng có NQ=ED/2
Ta có :MP=PQ
\Leftrightarrow ED2=BC−ED2ED2=BC−ED2
\Leftrightarrow ED=BC-ED
\Leftrightarrow 2ED=BC
Tương tự với NQ và PQ cũng rứa
Vậy muốn NQ=PQ=MP thì 2ED=BC Điều này là hiển nhiên ở (*)
từ đó phát triển lên câu a)NQ=PQ=MP=1/2ED
\Rightarrow MN=3/2ED \RightarrowMN=3/4BC
Đúng thì thanks giùm nha

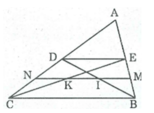
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
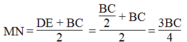
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC

Con tham khảo tại link dưới đây nhé:
Câu hỏi của Dương Ánh Ngọc - Toán lớp 8 - Học toán với OnlineMath

:a,nối E với D,ED là đường trung bình nên ED=4cm
MN là đường trung bình hình thang BEDC nên MN=(8+4):2=6
b,vì MI // ED và M là trung điểm BE => MI là đường trung bình ∆BED
MI=1/2 ED,tương tự ta có KN=MI=1/2 ED (*)
vì ED=1/2 BC mà ∆EDG∞∆IKG∞CBG(G là giao 2 tiếp tuyến)
nên IK=1/2 ED <=> kết hợp với(*)ta có KN=MI=IK=1/2ED
Bài2:gọi đoạn nối trung điểm 2 cạnh AB và AC của tứ giác ABCD là MN,ta có MN=1/2 BC,trong ∆BCD có BC<BD+CD nên MN< BD+CD(bất đẳng thức tam giác)
Bai3:gọi tứ giác đó là ABCD,MN là cạnh nối trung điểm,kéo dài AN giao DC tại E,ta có AB=CE ,nên ta có ∆ABN=∆CEN =>gocBAN=góc CEN.Mà 2 góc nằm ở vị trí so le trong nên AB // DC => ABCD là hình thang.
Bai4:a,kẻ BK // AD,ta có hình bình hành ABKD =>IE là hiệu 2 đáy,kẻ đường cao BH',ta có ∆BCH'=∆ADH,mà ∆BIE cân nên H' là trung điểm IE =>HD=1/2(DE-AB)
b,kẻ BG // với AC,ta có hình bình hành ABGC =>AB=CG
vì ABH'H là hình vuông=>AB=HH'=>HH'=CG mà H'C=DH nên ta có
HH'+H'C=CG+DH mà (HH'+H'C)+(CG+DH)=DG=DC+AB
=>HH'+H'C=HC=1/2(DC+AB)
Bài5:Từ M kẻ MM' vuông góc với d,ta có MM'//BB'//CC'
mà M là trung điểm BC nên MM' là đường trung bình hình thang BB'C'C,ta lại có O là trung điểm AM=>∆AA'O=∆MM'O nên AA'=MM'
ta có MM'=AA'=(BB'+CC'):2
Bài6:Kẻ MN//AB//DC =>MN=(7+3)/2=5 =>∆ANM và∆DNM cân tại N
góc AMN=(180độ-gócANM)/2
góc DMN=(180độ-gócDNM)/2
góc AMN+góc DMN=(180độ-gócANM+180độ-gócDNM)/2
=(360độ-180độ)/2=90độ=gócAMD=>AM vuông góc với DM
còn 3 bài cuối bác nào khỏe tay thì giúp cháu nó hộ em với,em mỏi tayquá rồi
Chi tiết thêm:
lâu lắm mới vào lại câu này
Bài7:từ C kẻ đường vuông góc với BE tại M
kéo dài CM giao AB tại N
Ta có ∆CME đồng dạng với ∆CAN (gg)
=>góc CEM= góc CNA
vì góc CEM= góc AEB (đối đỉnh)
=> góc CNA= góc AEB
=>∆CAN=∆BAE(góc nhọn,cạnh góc vuông,góc 90º)
=>AE=AN=AD
vì AN=AD
mà AK // CN
=> AK là đường trung bình hình thang CIDN
=>IK=KC
Trong tam giác ABC ta có:
E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ED//BC⇒ED//BC và ED=\(\frac{1}{2}BC\) (tính chất đường trung bình của tam giác)
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung bình hình thang BCDE ⇒ MN // DE
\(MN=\frac{DE+BC}{2}=\frac{\frac{BC}{2}+BC}{2}=\frac{3BC}{4}\)(tính chất đường trung bình hình thang)
Trong tam giác BED ta có:
M là trung điểm của BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
\(\Rightarrow MI=\frac{1}{2}DE=\frac{1}{4}BC\)(tính chất đường trung bình tam giác)
Trong tam giác CED ta có:
N là trung điểm của CD
NK // DE
Suy ra: NK là đường trung bình của ∆ BED
\(\Rightarrow NK=\frac{1}{2}DE=\frac{1}{4}BC\)(tính chất đường trung bình tam giác)
\(IK=MN-\left(MI+NK\right)\)
\(=\frac{3}{4}BC-\left(\frac{1}{4}BC+\frac{1}{4}BC\right)=\frac{1}{4}BC\)
\(\Rightarrow MI=IK=KN=\frac{1}{4}BC\)
Chúc bạn học tốt !!!
Cảm ơn hoang viet nhat nhé, nhưng lời giải này không được cô giáo mình chấp nhận vì cô bảo chưa học đến đường trung bình của hình thang nên nếu mình làm thế trên bảng thì các bạn sẽ không hiểu.