Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

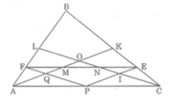
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL
Trong △ FPE ta có: PE//AK hay QM //PE
Suy ra: 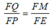 (định lí ta-lét) (1)
(định lí ta-lét) (1)
Trong △ ALO ta có:PF //CL hay FQ //LO
Suy ra: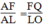 (định lí ta-lét) (2)
(định lí ta-lét) (2)
Trong △ ALC ta có: PF // CL
Suy ra: 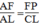 (định lí ta-lét) (3)
(định lí ta-lét) (3)
Từ (2) và (3) suy ra: 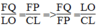
Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên 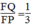 (4)
(4)
Từ (1) và (4) suy ra:  ⇒ FM = 1/3 FE
⇒ FM = 1/3 FE
Trong △ EPF ta có:PF // CL hay NI // PF
Suy ra:  (định lí ta –lét) (5)
(định lí ta –lét) (5)
Trong △ CKO ta có: EI // OK
Suy ra: 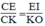 (định lí ta –lét) (6)
(định lí ta –lét) (6)
Trong △ CKA ta có:PE // AK
Suy ra: 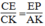 (định lí ta –lét) (7)
(định lí ta –lét) (7)
Từ (6) và (7) suy ra: 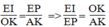
Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên 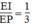 (8)
(8)
Từ (5) và (8) suy ra: 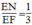 ⇒EN = 1/3 EF
⇒EN = 1/3 EF
Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF
Vậy EN = MN = NF

Lời giải:
a) Áp dụng định lý Talet cho:
Tam giác $CFD$ có $AM\parallel FD$:
$\frac{DF}{AM}=\frac{CD}{CM}(1)$
Tam giác $ABM$ có $ED\parallel AM$:
$\frac{ED}{AM}=\frac{BD}{BM}(2)$
Lấy $(1)+(2)\Rightarrow \frac{DE+DF}{AM}=\frac{CD}{BC:2}+\frac{BD}{BC:2}=\frac{BC}{BC:2}=2$
$\Rightarrow DE+DF=2AM$
Vì $AM$ không đổi khi $D$ di động nên $DE+DF$ không đổi khi $D$ di động
b) Dễ thấy $KADM$ là hình bình hành do có các cặp cạnh đối song song. Do đó $KA=DM$
Áp dụng định lý Talet cho trường hợp $AK\parallel BD$:
$\frac{KE}{ED}=\frac{KA}{BD}=\frac{DM}{BD}(3)$
Lấy $(1):(2)$ suy ra $\frac{DF}{ED}=\frac{CD}{BD}$
$\Rightarrow \frac{EF}{ED}=\frac{CD}{BD}-1=\frac{CD-BD}{BD}=\frac{CM+DM-(BM-DM)}{BD}=\frac{2DM}{BD}(4)$
Từ $(3);(4)\Rightarrow \frac{2KE}{ED}=\frac{EF}{ED}$
$\Rightarrow 2KE=EF\Rightarrow FK=EK$ hay $K$ là trung điểm $EF$
