Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ - AB = AC ( gt )
ABM = ACM vì { - AM chung
(c.c.c) - MB = MC ( m là trung điểm )
b/ AB // DC k phải AB // BC
T/g ABM = t/g DCM ( c.g.c)
AM = DM ( gt )
Góc AMB = DMC ( đđ )
BM = CM ( gt )
Có ABM = DCM ( t/g ABM = t/g DCM )
Lại ở vị trí slt
=> AB // DC
c/
AB = AC ( gt )
=> ABC cân tại A
Có AM là trung tuyến ( m là trug điểm )
=> AM là đường cao ABC
=> AM vuông góc BC

a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AB=CD và AB//CD
=>AC vuông góc CD
b: ABCD là hình bình hành
=>AD//BC và AD=BC

a) Xét tam giác AMB và tam giác AMC ta có:
AM chung
AB=AC (gt)
MB=MC (vì M là trung điểm của BC)
Suy ra tam giác AMB=tam giác AMC (c-c-c) (đpcm)
b) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc BAM=góc CAM (2 góc tương ứng)
Suy ra AM là tia phân giác của góc BAC (đpcm)
c) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc AMB=góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=180 độ (2 góc kề bù)
Suy ra góc AMB=góc AMC=180 độ/2=90 độ
Suy ra AM vuông góc với BC tại M (đpcm)
Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc ACM=góc ABM (2 góc tương ứng) (đpcm)

a:
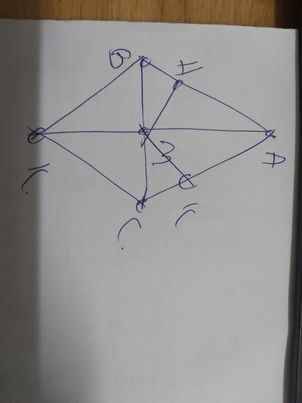
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABMH có
I là trung điểm của AM
I là trung điểm của BH
Do đó: ABMH là hình bình hành
Suy ra; AH//BM
hay AH//BC
a) Xét △ABM và △ACM có
AB = AC (gt)
AM : cạnh chung
BM = CM (M là trung điểm BC)
=> △ABM = △ACM (c.c.c)
b) Vì △ABC có AB = AC (gt)
=> △ABC cân tại A
=> △ABC có góc B = góc C