Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

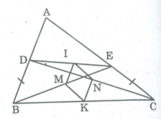
*Trong ∆ BCD,ta có:
K là trung điểm của BC (gt)
N là trung điểm của CD (gt)
Nên NK là đường trung bình của ∆ BCD
⇒ NK // BD và NK = 1/2 BD (1)
*Trong ∆ BED,ta có:
M là trung điểm của BE (gt)
I là trung điểm của DE (gt)
Nên MI là đường trung bình của ∆ BED
⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)
Từ (1) và (2) suy ra: MI // NK và MI = NK
Nên tứ giác MKNI là hình bình hành.
*Trong ∆ BEC ta có MK là đường trung bình.
⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)
BD = CE (gt). Suy ra: MK = KN
Vậy hình bình hành MKNI là hình thoi.
⇒IK ⊥ MN (t/chất hình thoi).


Áp dụng định lí về đường trung bình của tam giác để chứng minh MI = IN = NK = KM (cùng bằng \(\dfrac{BD}{2}\) và \(\dfrac{CE}{2}\) )
MINK là hình thoi nên \(IK\perp MN\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

xét tg BD E có: I là t/đ của DE(gt) và M la t/đ của BE (gt) => MI là đg trung bình của tg BDE => MI= 1/2. BD
c/m tương tự ta đc: IN là đg trung bình của tg DEC => IN=1/2.EC
MK là đg trung bình của tg BEC => MK=1/2.EC
NK là đg trung bình của tg BDC=> NK=1/2.BD
Mà BD=CE (gt) nên MI=IN=MK=NK => tg MKNI là hthoi => MN vuông góc vs IK (t/c 2 đg chéo của hthoi)

Bài 1:
a: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường cao
nên AB là phân giác của góc EAD(1)
Ta có: D và F đối xứng nhau qua AC
nên AD=AF
=>ΔADF cân tại A
=>AC là phân giác của góc DAF(2)
Từ (1) và (2) suy ra góc EAF=2xgóc BAC=120 độ
AE=AD
AF=AD
Do đó: AE=AF
b: Xét ΔADM và ΔAEM có
AD=AE
góc DAM=góc EAM
AM chung
DO đó: ΔADM=ΔAEM
SUy ra: góc ADM=góc AEM(3)
Xét ΔADN và ΔAFN có
AD=AF
góc DAN=góc FAN
AN chung
Do đó; ΔADN=ΔAFN
Suy ra: góc ADN=góc AFN(4)
Từ (3) và (4) suy ra góc ADM=góc ADN
hay DA là phân giác của góc MDN