Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

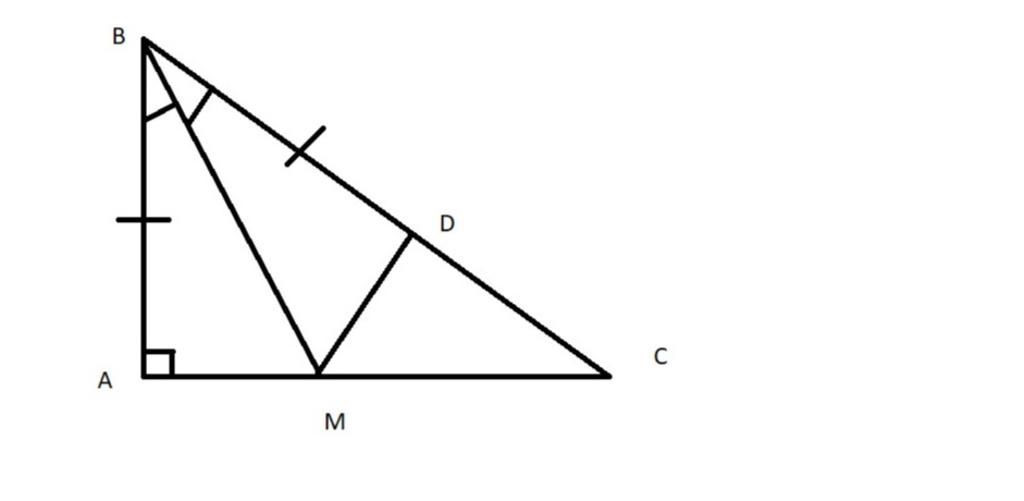

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA

Bài 1 a, xét tam giác ABD và tam giác HBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{HBD}\)(gt)
\(\Rightarrow\)tam giác ABD = tam giác HBD( CH-GN)
\(\Rightarrow\)AB=HB
b,trên tia đối của tia DH lấy O sao cho HD=DO
xét tam giác ADO và tam giác CDH có:
DH=DO( theo trên)
\(\widehat{ADO}\)=\(\widehat{CDH}\)( Vì đối đỉnh)
\(\Rightarrow\)tam giác ADO=tam giác CDH( CH-GN)\(\Rightarrow\)AD=CD

Câu 1:
A B C H D
a) So sánh ∠B và ∠C ?
Vì AB < AC (gt) ⇒ ∠C < ∠B
b) So sánh BH và CH ?
Trên ta BC lấy điểm D sao cho BH = HD
Xét hai tam giác vuông ABH và ADH có:
BH = DH (gt)
AH : cạnh chung
Do đó: ΔABH = ΔADH (hai cạnh góc vuông)
⇒ BH = HD (hai cạnh tương ứng)
Mà CH = CD + DH ( do D nằm giữa H và C)
⇒ CH > BH .
Câu 2 để tớ đi học về rồi làm cho ~