Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu sai nha bạn người ta bảo điều kiện của tam giác abc chứ ko phải thay canh BE với CE nha

Chẳng hiểu gì.Hỏi cô Thủy hoặc thầy Phong hoặc thầy Huy.Không thì vào goodgle.

Xét \(\Delta BEM\) và \(\Delta CFM\) có:
\(\widehat{E}=\widehat{F}=90^o\)
MB = MC (gt)
\(\widehat{BME}=\widehat{CMF}\) (đối đỉnh)
Do đó \(\Delta BEM=\Delta CFM\) (cạnh huyền - góc nhọn)
=> BE = CF (2 cạnh t/ứ)
Xét \(\Delta BEM\)và \(\Delta CFM\)
\(\widehat{E}=\widehat{F}=90^{ }\)độ
\(MB=MC\)( gt )
\(\widehat{BME}=CMF\)( đối đỉnh )
\(\Rightarrow\)\(\Delta BEM=\Delta CFM\)( g - c - g )
\(\Rightarrow\)\(BE=CF\)( 2 cạnh tương ứng bằng nhau )

xét tam giác vuông BEC có EM là đường trung tuyến ứng với cạnh huyền
suy ra EM = \(\frac{1}{2}\)BC (1)
xét tam giác vuông CFB có FM là đường trung tuyến ứng với cạnh huyền
suy ra FM = \(\frac{1}{2}\)BC (2)
từ (1) và (2) suy ra M là trung điểm EF
mà M là trung điểm của BC
từ 2 điều đó suy ra BECF là hình bình hành
suy ra BE = CF

a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF

Kí hiệu tam giác là t/g nhé
a) Có: BE _|_ Ax (gt)
CF _|_ Ax (gt)
Suy ra BE // CF (1)
Xét t/g EMB vuông tại E và t/g FMC vuông tại F có:
BM = CM (gt)
EMB = FMC ( đối đỉnh)
Do đó, t/g EMB = t/g FMC ( cạnh huyền và góc nhọn kề)
=> BE = CF (2 cạnh tương ứng) (2)
ME = MF (2 cạnh tương ứng) (3)
(1); (2) và (3) là đpcm
b) Xét t/g EMC và t/g FMB có:
EM = MF (câu a)
EMC = FMB ( đối đỉnh)
CM = BM (gt)
Do đó, t/g EMC = t/g FMB (c.g.c)
=> CE = BF (2 cạnh tương ứng) (4)
ECM = FBM (2 góc tương ứng)
Mà ECM và FBM là 2 góc so le trong
Nên EC // BF (5)
(4) và (5) là đpcm

Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)
Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)

Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBEM=ΔCFM

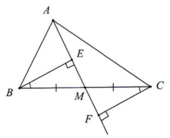
a, Ta có: BE vuông Ax(1)
CF vuông Ax(2)
Từ (1) và (2) => BE//CF
b,Tam giác BEM = Tam giác CFM(g.c.g)
=>BE=CF(các cạnh tương ứng)
Chứng minh tương tự ta đươc: Tam giác CME = Tam giác BMF (c.g.c)
=> CE=BF(các cạnh tương ứng)
c,Nếu BE=CE
thì tam giác BEC cân tại E
mà E thuộc AM
AM là đg trug tuyến
thì khi cân cũng sẽ là đg cao
nên khi tam giác ABC cân tại A THÌ BE=CE
lên vietjack có cách giải chi tiết