Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k
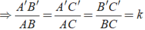
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
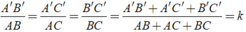
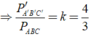
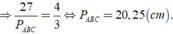

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

Lời giải:
a. $\triangle A'B'C'\sim \triangle ABC$ theo tỉ số $k$
$\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$
$\Rightarrow A'B'=kAB; B'C'=kBC; C'A'=kCA$
$\Rightarrow A'B'+B'C'+C'A'=k(AB+BC+AC)$
$\Rightarrow P_{A'B'C'}=kP_{ABC}$
$\Rightarrow \frac{P_{A'B'C'}}{P_{ABC}}=k$
b.
Chu vi tam giác ABC:
$40:(5-3).3=60$ (dm)
Chu vi tam giác A'B'C':
$40:(5-3).5=100$ (dm)

`a) ΔA'B'C' ∼ ΔABC` theo tỉ lệ đồng dạng `k = 2/5`
`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = 2/5`
Theo tính chất dãy tỉ số bằng nhau
`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = (A'B' + A'C' + B'C')/(AB + AC + BC) = 2/5`
`=> (PΔA'B'C')/(PΔABC) = 2/5`
b) Từ a) ta có: `(PΔA'B'C')/(PΔABC) = 2/5`
`=> (PΔA'B'C')/2 = (PΔABC)/5`
Áp dụng tính chất dãy tỉ số bằng nhau:
`=> (PΔA'B'C')/2 = (PΔABC)/5 = (PΔABC - PΔA'B'C')/(5-2) = 30/3 = 10`
`=> PΔA'B'C' = 10 xx 2 = 20 (cm)`
`PΔABC = 10 xx 5 = 50 (cm)`

@@@@
Em không bt đúng hay sai đúng thì tíc không đúng thì thôi . Em mong là đúng
tam giác ABC có MN thuộc AB ; PQ thuộc AC ; Ab =12 ;AC=16; Am=3; AN=6 ; AP=2 ; AQ=4 thì 2 đường thẳng nào song song
HT

Do 2 tam giác A'B'C' đồng dạng với tam giác ABC nên 2 tam giác này bằng nhau
=> A'B'=AB ; B'C'=BC ; A'C'=AC
Nên A'B'+B'C'+A'C'=AB+AC+BC ( theo công thức tính chu vi tam giác)
Nên chu vi 2 tam giác trên bằng nhau
tam giác ABC đồng dạng tam giác A'B'C'
=> \(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}=k\)
áp dụng tính chất day tỉ số bằng nhau có:
\(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}=\frac{AB+BC+AC}{A'B'+B'C'+A'C'}=k\)
=> \(\frac{Chuvi_{\Delta ABC}}{Chuvi_{\Delta}A'B'C}=k\) (đpcm)
Chịu khó tự vẽ hình chút nhoa!
Vì tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng K= \(\dfrac{2}{3}\) nên ta có:
\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\)\(=\dfrac{2}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\)
\(=\)\(\dfrac{A'B'+B'C'+A'C'}{AB+BC+AC}\) \(=\dfrac{C_{A'B'C'}}{C_{ABC}}\)\(=\dfrac{2}{3}\)
⇒ \(\dfrac{C_{A'B'C'}}{12}=\dfrac{2}{3}\) ⇒ CA'B'C' = 8 (cm)
Vậy chu vi tam giác A'B'C' bằng 8 cm