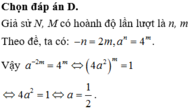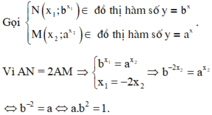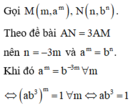Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

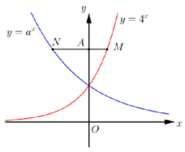
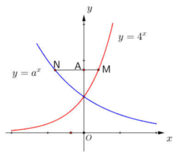
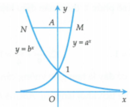
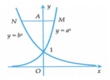
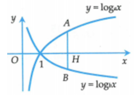
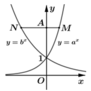
Gọi A(0;t) với t > 0. Suy ra 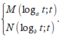
Theo giả thiết AN = 2AM nên suy ra
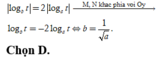

Đáp án B.
Phương trình đường thẳng d : y = m x + 2 + 2 .
Phương trình hoành độ giao điểm của và d:
2 x + 1 x − 1 = m x + 2 + 2 ⇒ m x 2 + m x − 2 m − 3 = 0 (*).
Để (H) và d cắt nhau tại hai điểm phân biệt thì (*) phải có hai nghiệm phân biệt ⇔ m ≠ 0 Δ > 0 ⇔ m ≠ 0 9 m 2 + 12 > 0 (**). Gọi là hai nghiệm của (*).
Khi đó M = x 1 ; m x 1 + 2 + 2 , N = x 2 ; m x 2 + 2 + 2 .
Hai cạnh của hình chữ nhật tạo bởi bốn đường thẳng như đã cho trong bài là x 2 − x 1 và m x 2 − x 1 . Hình chữ nhật này là hình vuông khi và chỉ khi m x 2 − x 1 = x 2 − x 1 ⇔ m = 1 ⇔ m = ± 1 . Ta thấy chỉ có M=1 thỏa mãn (**).
Vậy chỉ có một giá trị của m thỏa mãn yêu cầu bài toán. Chọn đáp án B.