O
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
17 tháng 6 2017
Đáp án D
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là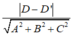 
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi:
A 2 + B 2 + C 2 =1
Do đó, mệnh đề D có thể sai.
CM
29 tháng 11 2019
Đường thẳng d đi qua M 0 và có vecto chỉ phương n P → (A; B; C)
Do đó phương trình tham số của d là:
CM
18 tháng 8 2018
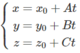
Do (P) và (Q) cắt nhau nên n P → ∧ n Q → ≠ 0 → . Đường thẳng d đi qua M 0 và có vecto chỉ phương
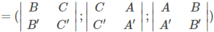
Do đó phương trình tham số của d là:
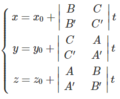
Đặc biệt phương trình trên cũng là phương trình đường thẳng là giao của hai mặt phẳng cắt nhau (P): Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0 với M 0 là điểm chung của (P) và (Q).
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 5 2020
19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 5 2020
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)
LV
1
11 tháng 4 2023
vecto u=(3;-1;2)
=>vecto v=(2;3;-1,5)
vecto AB=(6;2;-1)
Phương trình mặt phẳng cần tìm là:
2(x-6)+3(y-2)-1,5(z+1)=0
=>2x-12+3y-6-1,5z-1,5=0
=>2x+3y-1,5z=19,5
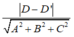
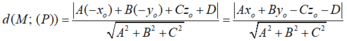
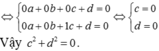
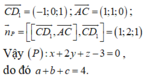
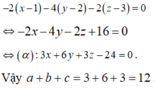
ta tìm được điểm A ( a1, a2,a3) không nằm trong mp :)
tìm đươc 1 vecto pháp tuyến của mp là n = (a,b,c).
tui lo lắng các bác ham điểm không trả lời nên để tạm luôn ở đây, mai tui quay lại xem bài của tui.
gửi câu hỏi rồi tự trả lời 😑