K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
Đoàn Đức Hà
Giáo viên
13 tháng 7 2021
\(y^2=x\left(x+1\right)\left(x+7\right)\left(x+8\right)\)
\(=\left(x^2+8x\right)\left(x^2+8x+7\right)\)
\(\Rightarrow4y^2=\left(2x^2+16x\right)\left(2x^2+16x+14\right)\)
\(=\left(2x^2+16x+7-7\right)\left(2x^2+16x+7+7\right)\)
\(=\left(2x^2+16x+7\right)^2-49\)
\(\Leftrightarrow\left(2x^2+16x+7\right)^2-4y^2=49\)
\(\Leftrightarrow\left(2x^2+16x+7-2y\right)\left(2x^2+16x+7+2y\right)=49=1.49=7.7\)
Xét các trường hợp và thu được các nghiệm là: \(\left(-3,0\right),\left(0,0\right)\).
SP
1
KV
15 tháng 8 2023
x/y = 2/5 ⇒ x/2 = y/5
⇒ x/5 = 2y/10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/2 = 2y/10 = (x + 2y)/(2 + 10) = 36/12 = 3
x/2 = 3 ⇒ x = 2 . 3 = 6
y/5 = 3 ⇒ y = 5 . 3 = 15
Vậy x = 6; y = 10
AH
Akai Haruma
Giáo viên
15 tháng 8 2023
Tính giá trị của $x+y-2=0$ là sao nhỉ? $x+y-2=0$ sẵn rồi mà bạn?
IC
1
3 tháng 8 2020
+) \(\sqrt[3]{x+1}+\sqrt[3]{x-1}=\sqrt[3]{5x}\left(1\right)\)
+) Lập phương 2 vế ta được :
\(2x+3\sqrt[3]{x^2-1}\left(\sqrt[3]{x+1}+\sqrt[3]{x-1}\right)=5x\left(2\right)\)
Thay ( 1 ) vào ( 2 ) ta có :
\(\sqrt[3]{x^2-1}.\sqrt[3]{5x}=x\)
\(\Rightarrow4x^3-5x=0\)
\(\Rightarrow\hept{\begin{cases}x=0\\x=\pm\frac{\sqrt{5}}{2}\end{cases}}\)
P/s : ko có tgian làm full . Thông cảm nhen ^-^
4 tháng 4 2020
Mẹo thì không có đâu bạn ạ! ^_^. Cơ bản là bạn phải hiểu vấn đề của bài thôi!
4 tháng 4 2020
Bạn thử lên youtube học của THẦY QUANG thử xem
Thầy này dạy dễ hiểu lắm
NU
0
KV
29 tháng 12 2022
a) ĐKXĐ:
x³ - 1 khác 0
x khác 1
b) A = (5x² + 5x + 5)/(x³ - 1)
= 5(x² + x + 1)/[(x - 1)(x² + x + 1)]
= 5/(x - 1)
Thay x = 7 vào A, ta được:
A = 5/(7 - 1)
= 5/6
KV
29 tháng 12 2022
a) (2x - 7)/4x + (3 + 4x)/4x
= (2x - 7 + 3 + 4x)/4x
= (6x - 4)/4x
= (3x - 2)/2x
b) (9x - 5)/(x² + x) + (10 - 4x)/(x² + x)
= (9x - 5 + 10 - 4x)/[x(x + 1)]
= (5x + 5)/[x(x + 1)]
= 5(x + 1)/[x(x + 1)]
= 5/x
c) (3x - 9)/(x - 1) : (x² - 9)/(x² - 2x + 1)
= 3(x - 3)/(x - 1) . (x - 1)²/[(x - 3)(x + 3)
= 3(x - 1)/(x + 3)
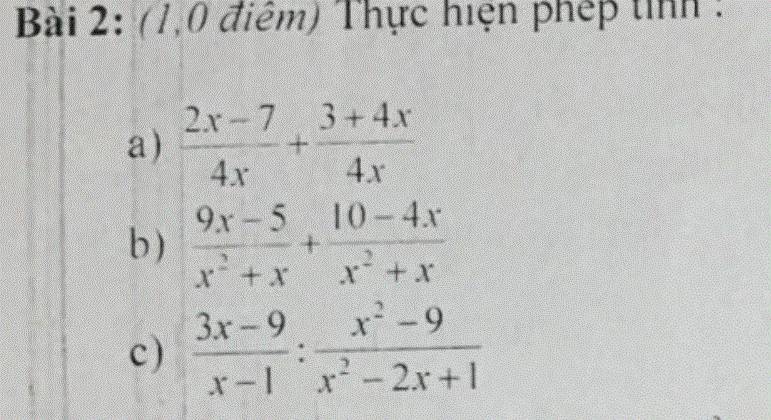
`Answer:`
\(\frac{\left(m^2+1\right).x+1-2m^2}{x-5}\)\(=2m\left(ĐKXĐ:x\ne5\right)\)
`=>(m^2+1).x+1-2m^2=2m.(x-5)`
`<=>(m^2-2m+1).x=2m^2-10m-1`
`<=>(m-1)^2``x=2m^2-10m-1(1)`
Phương trình `(1)` có nghiệm duy nhất `<=>m\ne1`
Lúc đó nghiệm của phương trình `(1)` sẽ là \(x=\frac{2m^2-10m-1}{\left(m-1\right)^2}\)
Ta xét hiệu:
\(x-3=\frac{2m^2-10m-1}{\left(m-1\right)^2}-3\)
\(=\frac{2m^2-10m-1-3\left(m-1\right)^2}{\left(m-1\right)^2}\)
\(=\frac{-m^2-4m-4}{\left(m-1\right)^2}\)
\(=-\frac{\left(m+2\right)^2}{\left(m-1\right)^2}\)
\(\le0;\forall m\ne1\)
\(\Rightarrow x-3\le0;\forall m\ne1\)
\(\Rightarrow x\le3;\forall m\ne1\)
Dấu "=" xảy ra khi `m+2=0<=>m=-2`