Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo định lí Viet thì \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1.x_2=\left(3m-3\right)^2\end{matrix}\right.\)
\(\dfrac{16}{9}.x_1.x_2=\dfrac{16}{9}.\left(3m-3\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left[\dfrac{4}{3}.\left(3m-3\right)\right]^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(4m-4\right)^2\)
⇒ \(\dfrac{16}{9}.x_1.x_2=\left(x_1+x_2-4\right)^2\)
Đối chiếu ⇒ \(\left\{{}\begin{matrix}a=-4\\b=\dfrac{16}{9}\end{matrix}\right.\)
⇒ \(\dfrac{b}{a}=\dfrac{-4}{9}\)
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
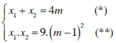
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
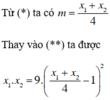
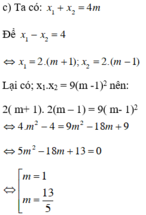
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành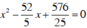 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
Hình như đề thiếu, pt: \(x^2-\left(m+1\right)x+m-2=0\)
Phương trình đã cho có nghiệm khi \(\Delta=\left(m+1\right)^2-4\left(m-2\right)=m^2-2m+9>0\)
\(\Rightarrow\) Phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị m
Định lí Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m-2\end{matrix}\right.\)
a, Theo giả thiết ta có: \(x_1^2+x_2^2=100\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=100\)
\(\Leftrightarrow\left(m+1\right)^2-2\left(m-2\right)=100\)
\(\Leftrightarrow m^2+2m+1-2m+4=100\)
\(\Leftrightarrow m^2=95\)
\(\Leftrightarrow m=\sqrt{95}\)
b, \(P=\left|x_1-x_2\right|\)
\(P^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(m+1\right)^2-4\left(m-2\right)\)
\(=m^2-2m+9=\left(m-1\right)^2+8\ge8\)
\(\Rightarrow P=\left|x_1-x_2\right|\ge2\sqrt{2}\)
\(minP=2\sqrt{2}\Leftrightarrow m=1\)
Phương trình ⇔ 4 x − 17 ≥ 0 x 2 − 4 x − 5 = 4 x − 17 2
⇔ x ≥ 17 4 x 2 − 5 x − 5 2 = 4 x − 17 2
⇔ x ≥ 17 4 ( x 2 − 8 x + 12 ) ( x 2 − 22 ) = 0 ⇔ x ≥ 17 4 x 2 − 8 x + 12 = 0 x 2 − 22 = 0
⇔ x ≥ 17 4 x = 2 ∨ x = 6 x = ± 22 ⇔ x = 6 x = 22 ⇒ P = 22 2 + 6 = 28
Đáp án cần chọn là: C
Khi đó phương trình trở thành:
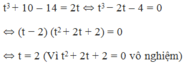
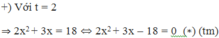
Giả sử x 1 , x 2 là hai nghiệm của phương trình (*)
Theo Vi – et, ta có x 1 + x 2 = − 3 2 x 1 . x 2 = − 9
⇒ A = x 1 2 + x 2 2 − 4 x 1 x 2 = x 1 + x 2 2 − 6 x 1 . x 2 = 9 4 + 54 = 225 4 = 15 2
Đáp án cần chọn là: D
Đk để pt trên có 2 nghiệm phân biệt x1,x2 : a>0 và denta>0
suy ra denta= (2m+1)^2-4.(m^2+1)>0
suy ra : m>3/4
Ta có P=x1x2/x1+x2=(m^2+1)/(2m+1)
Ta có: P∈Z
⇒4P∈Z
⇒(4m^2+4)/2m+1=(2m-1)+5/2m+1∈Z
⇒2m+1=Ư(5)={−5;−1;1;5}
⇒m={−3;−1;0;2}
Kết hợp đk m>3/4 ta được m=2
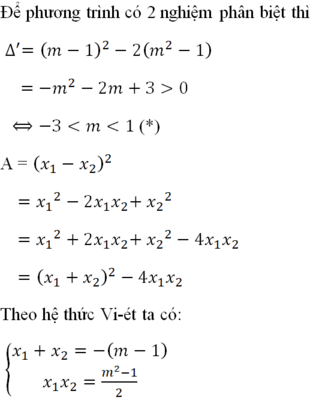
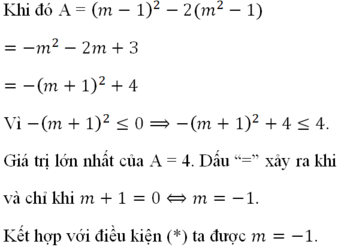
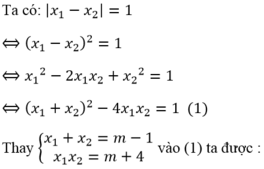
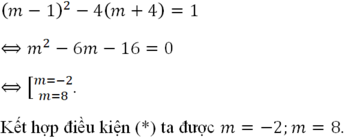
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=a\\x_1x_2=1\end{matrix}\right.\)
\(A=x_1^5+x_2^5=\left(x_1^2+x_2^2\right)\left(x_1^3+x_2^3\right)-x_1^2x_2^2\left(x_1+x_2\right)\\ \Leftrightarrow A=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]-a\\ \Leftrightarrow A=\left(a^2-2\right)\left(a^3-3a\right)-a\\ \Leftrightarrow A=a^5-5a^3+5a\)