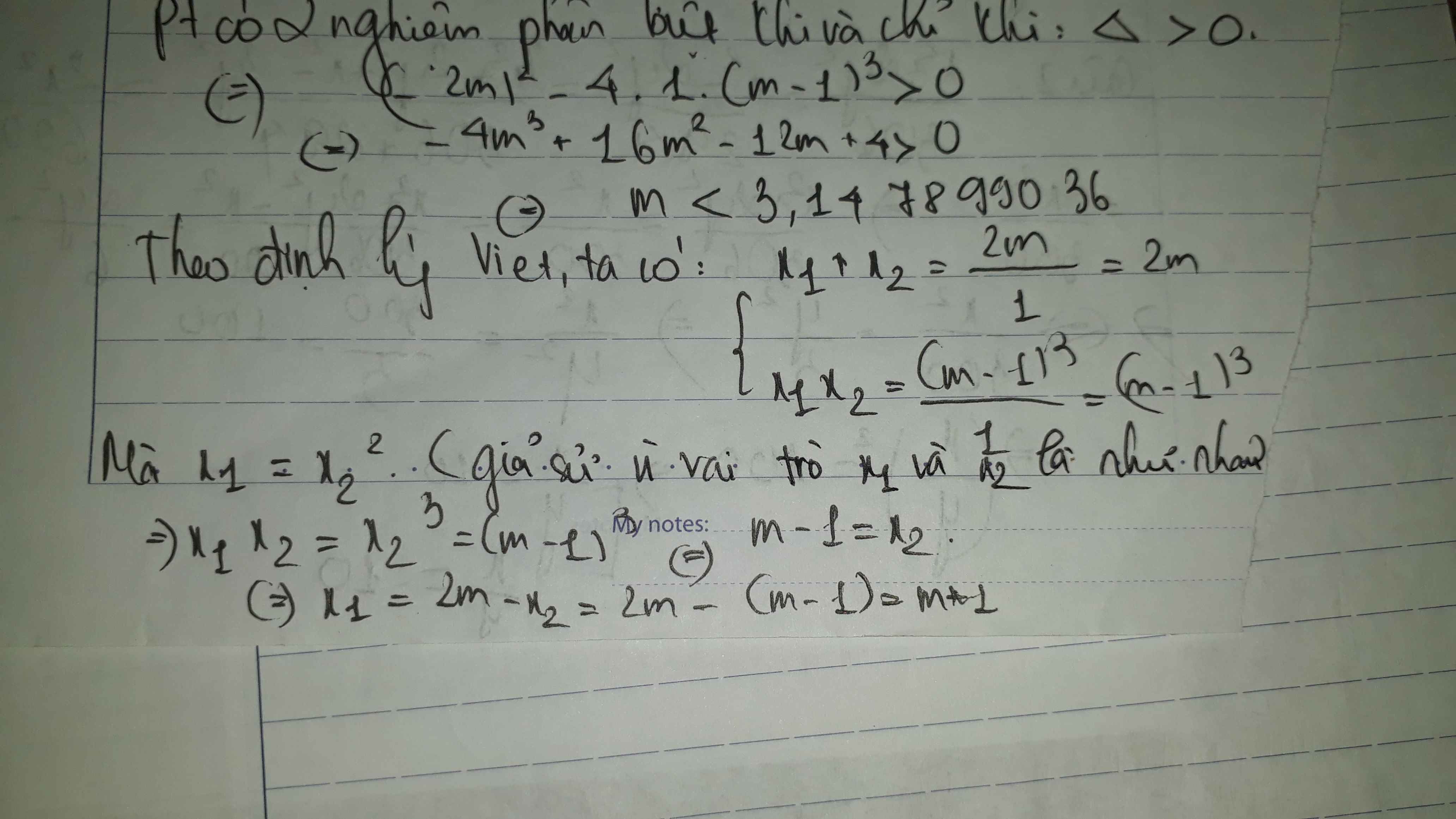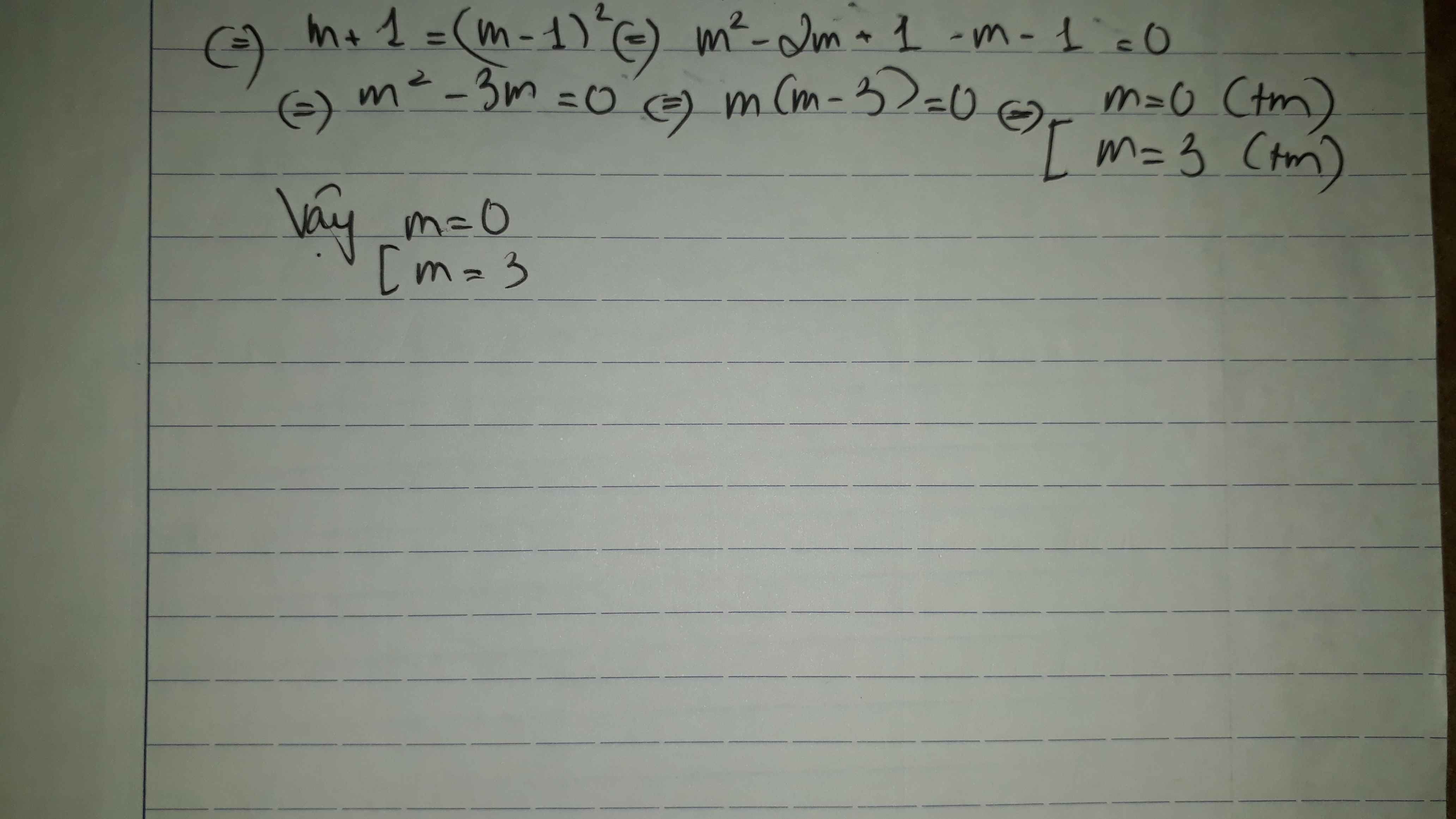Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2-2mx+\left(m-1\right)^3=0\left(1\right)\)
PT (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta'=m^2-\left(m-1\right)^3>0\)(*)
Giả sử phương trình có 2 nghiệm phân biệt là u, u2 thì theo Vi-et ta có:
\(\hept{\begin{cases}u+u^2=2m\\u\cdot u^2=\left(m-1\right)^2\end{cases}}\)(**)
(**)\(\Leftrightarrow\hept{\begin{cases}u+u^2=2m\\u^3=\left(m-1\right)^3\end{cases}\Leftrightarrow\hept{\begin{cases}u+u^2=2m\\u=m-1\end{cases}\Leftrightarrow}\hept{\begin{cases}m-1+\left(m-1\right)^2=2m\\u=m-1\end{cases}\Leftrightarrow}\hept{\begin{cases}m^2-3m=0\\u=m-1\end{cases}}}\)
PT \(m^2-3m=0\Leftrightarrow m\left(m-3\right)=0\Leftrightarrow m_1=0;m_2=3\left(tmđk\right)\)
Vậy m=0; m=3 là 2 giá trị cần tìm

- \(\Delta^'=m^2-\left(m-1\right)\left(m+1\right)=m^2-m^2+1=1>0\)vậy phương trình luôn có hai nghiệm với mọi \(m\ne1\)
- Theo viet ta có : \(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=m+1\end{cases}}\)\(\Rightarrow m+1=5\Rightarrow m=4\Rightarrow x_1+x_2=2m=2.4=8\)
- từ hệ thức viet ta khử m được hệ thức liên hệ giữa 2 nghiệm ko phụ thuộc m: thấy \(x_1+x_2-2x_2x_1=2m-2\left(m+1\right)=-2\)
- \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=-\frac{5}{2}\Leftrightarrow\frac{x_1^2+x_2^2}{x_1x_2}=-\frac{5}{2}\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=-\frac{5}{2}\)\(\Leftrightarrow\frac{4m^2-2m-2}{m+1}=-\frac{5}{2}\Rightarrow8m^2-4m-4=-5m-5\left(m\ne-1\right)\)\(\Leftrightarrow8m^2+m+1=0\left(vn\right)\)không có giá trị nào của m thỏa mãn

Để phương trình trên có 3 nghiệm phân biệt thì phương trình \(x^2-2mx-m=0\left(1\right)\) phải có hai nghiệm phân biệt khác 1.
Trong 3 nghiệm phải có 2 nghiệm dương mà x = 1 là một nghiệm dương rồi nên phương trình (1) phải có 1 nghiệm dương và một nghiệm âm, hay nói cách khác là hai nghiệm trái dấu.
Kết hợp các điều kiện ta có phương trình (1) phải có 2 nghiệm phân biệt khác 1 và trái dấu nhau. Điều kiện đó cho ta hệ sau:
\( \begin{cases} \Delta>0\\ P<0\\ 1-2m-m \neq 0\\ \end{cases} \Leftrightarrow \begin{cases} m^2+m>0\\-m<0\\ m \neq \dfrac{1}{3}\\ \end{cases} \Leftrightarrow \begin{cases} m<-1 \text{ hoăc } m>0\\m>0\\ m \neq \dfrac{1}{3}\\ \end{cases} \Leftrightarrow \begin{cases} m>0\\ m \neq \dfrac{1}{3}\\ \end{cases} \)
Chúc em học tập tốt :))
cô ơi ,cô viết cái j ở mấy dòng cuối thế ạ em xem chả hiểu cái j

a) Nếu m = -1 thì : \(4x-3=0\Leftrightarrow x=\frac{3}{4}\) => pt có một nghiệm
Nếu \(m\ne-1\) , xét \(\Delta'=\left(m-1\right)^2-\left(m+1\right)\left(m-2\right)=m^2-2m+1-\left(m^2-m-2\right)=-m+3\)
Để pt có hai nghiệm phân biệt thì \(\Delta>0\) , tức là \(3-m>0\Leftrightarrow m< 3\)
Vậy để pt có hai nghiệm phân biệt thì \(\begin{cases}m< 3\\m\ne-1\end{cases}\)
b) Thay x = 2 vào pt đã cho , tìm được m = -6
Suy ra pt : \(-5x^2+14x-8=0\Leftrightarrow\left(5x-4\right)\left(x-2\right)=0\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=2\\x=\frac{4}{5}\end{array}\right.\)
Vậy nghiệm còn lại là x = 4/5
c) Áp dụng hệ thức Vi-et , ta có : \(\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1.x_2=m-2\end{cases}\)
\(\frac{1}{x_1}+\frac{1}{x_2}=\frac{7}{4}\Leftrightarrow4\left(x_1+x_2\right)=7x_1.x_2\)
\(\Rightarrow4.\left(2m-2\right)=7.\left(m-2\right)\Leftrightarrow8m-8=7m-14\Leftrightarrow m=-6\)
d) Ta có : \(A=2\left(x_1^2+x_2^2\right)+x_1.x_2=2\left(x_1+x_2\right)^2-3x_1.x_2=8\left(m-1\right)^2-3\left(m-2\right)\)
\(=8m^2-19m+14=8\left(m-\frac{19}{16}\right)^2+\frac{87}{32}\ge\frac{87}{32}\)
=> Min A = 87/32 <=> m = 19/16